Упражнение 1150 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1150 учебника 2023-2025 (стр. 228):
Какую фигуру на координатной плоскости задаёт система неравенств:
а) \( \begin{cases} y \le x,\\ y \ge 7; \end{cases} \)
б) \( \begin{cases} y \le -x + 7,\\ y \ge -x + 1. \end{cases} \)
№1150 учебника 2013-2022 (стр. 227):
Докажите, что графику уравнения \(6x - 12y = 5\) не принадлежит ни одна точка с целочисленными координатами.
Подсказка
№1150 учебника 2023-2025 (стр. 228):
Вспомните:
- Что называют решением системы неравенств с двумя переменными.
- График линейной функции.
- Координаты точки.
- Сложение рациональных чисел.
- Что называют углом.
№1150 учебника 2013-2022 (стр. 227):
Вспомните:
- Уравнение с двумя переменными, его свойства.
- Вынесение общего множителя за скобки.
- Целые числа.
Ответ
№1150 учебника 2023-2025 (стр. 228):
а) \( \begin{cases} y \le x,\\ y \ge 7; \end{cases} \)
\(y = x\)
| \(x\) | 0 | 3 |
| \(y\) | 0 | 3 |
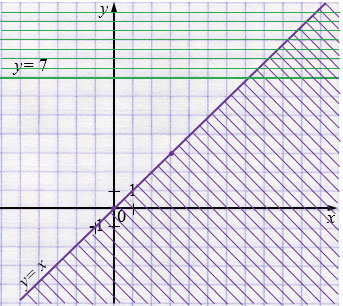
Ответ: угол.
б) \( \begin{cases} y \le -x + 7,\\ y \ge -x + 1. \end{cases} \)
\(y = -x + 7\)
| \(x\) | 0 | 7 |
| \(y\) | 7 | 0 |
\( y = -x + 1\)
| \(x\) | 0 | 1 |
| \(y\) | 1 | 0 |
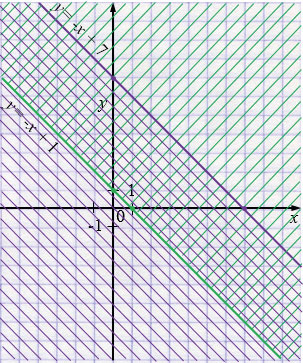
Ответ: полоса.
Пояснения:
Основные понятия и правила:
– Линейная функция \(y=kx+b\). Строится по двум точкам.
– Если прямые параллельны, пересечение задаёт полосу (между ними).
– Если прямые пересекаются, пересечение полуплоскостей даёт угол (с вершиной в точке пересечения).
Пояснения к случаю а):
– Линии \(y=x\) и \(y=7\) пересекаются в точке \( (7,7)\).
– Полуплоскость \(y\ge7\) лежит выше (или на) прямой \(y=7\), а \(y\le x\) — ниже (или на) прямой \(y=x\).
– Пересечение двух полуплоскостей ограничено двумя лучами, исходящими из точки \( (7,7)\), что дает угол.
Пояснения к случаю б):
– Прямые \(y=-x+7\) и \(y=-x+1\) параллельны.
– Полуплоскость \(y \le -x + 7\) лежит ниже (или на) прямой \(y = -x + 7\), а \(y \ge -x + 1\) — выше (или на) прямой \(y = -x + 1\).
– Пересечение двух полуплоскостей ограничено двумя параллельными прямыми, что дает полосу.
№1150 учебника 2013-2022 (стр. 227):
\(6x - 12y = 5\)
\(6\cdot(x - 2y)=5\) / \( : 6\)
\(x - 2y=\frac{5}{6}\)
\(x\) и \(y\) — целые числа, тогда выражение \(x-2y\) тоже целое число, а \(\frac{5}{6}\) не является целым числом, значит, графику не принадлежит ни одна точка с целочисленными координатами.
Пояснения:
– Если \(m\) целое, то \(6m\) обязательно делится на 6 и даёт остаток 0 при делении на 6.
– Число 5 при делении на 6 даёт остаток 5, то есть не может быть результатом деления на 6.
– Полученное противоречие означает, что нет целых \(x\) и \(y\), удовлетворяющих исходному уравнению.
– Метод доказательства основан на свойстве делимости.
Вернуться к содержанию учебника