Упражнение 1156 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник. Страница 228
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1156 учебника 2023-2025 (стр. 228):
Известно, что:
а) пара значений переменных \(x = 5\), \(y = 7\) является решением уравнения \(a x - 2y = 1\). Найдите коэффициент \(a\).
б) пара значений переменных \(x = -3\), \(y = 8\) является решением уравнения \(5x + b y = 17\). Найдите коэффициент \(b\).
№1156 учебника 2013-2022 (стр. 228):
Постройте график уравнения:
а) \(y = |x|\);
б) \(y = -|x|\).
Подсказка
№1156 учебника 2023-2025 (стр. 228):
Вспомните:
- Что называют решением линейного уравнения с двумя переменными.
- Линейное уравнение с одной переменной.
- Свойства уравнений.
- Деление и дроби.
- Умножение рациональных чисел.
№1156 учебника 2013-2022 (стр. 228):
Вспомните:
- График линейной функции.
- Модуль числа.
Ответ
№1156 учебника 2023-2025 (стр. 228):
а) \(a x - 2y = 1\)
\(x = 5\), \(y = 7\)
\[ 5a - 2\cdot7 = 1 \]
\[ 5a - 14 = 1 \]
\[ 5a = 1 + 14 \]
\[ 5a = 15 \]
\[ a = \frac{15}{5} \]
\[ a = 3 \]
Ответ: \( a = 3 \).
б) \(5x + b y = 17\)
\(x = -3\), \(y = 8\)
\[ 5\cdot(-3) + 8b = 17 \]
\[ -15 + 8b = 17 \]
\[ 8b = 17 + 15 \]
\[ 8b = 32 \]
\[ b = \frac{32}{8} = 4 \]
\[ b = 4 \]
Ответ: \( b = 4 \)
Пояснения:
– Для каждого случая подставили заданные значения \(x\) и \(y\) в уравнение.
– Выполнили умножение и вычитание (раскрытие скобок и вычисление произведений).
– Перенесли свободные члены в одну сторону, чтобы получить линейное уравнение вида \(ka = c\) (или \(kb = c\)).
– Разделили обе части на коэффициент при неизвестном, чтобы найти значение \(a\) или \(b\).
№1156 учебника 2013-2022 (стр. 228):
а) \(y = |x|\)
Если \(x\ge0\), то \(y = x\).
| \(x\) | 0 | 3 |
| \(y\) | 0 | 3 |
Если \(x<0\), то \(y = -x\).
| \(x\) | 0 | -3 |
| \(y\) | 0 | 3 |

б) \(y = -|x|\)
Если \(x\ge0\), то \(y = -x\).
| \(x\) | 0 | 3 |
| \(y\) | 0 | -3 |
Если \(x<0\), то \(y = -(-x)= x\).
| \(x\) | 0 | -3 |
| \(y\) | 0 | -3 |
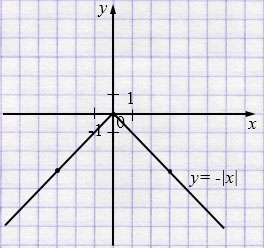
Пояснения:
– Функция задаётся по частям: \(|x|\) равен самому \(x\), если \(x\ge0\), и противоположному \(-x\), если \(x<0\).
– Каждый график представляет собой «угол» из двух лучей, являющихся биссектрисами координатных четвертей.
– В обеих функциях ключевая точка — вершина угла \((0;0)\).
Вернуться к содержанию учебника