Упражнение 296 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№296 учебника 2023-2025 (стр. 72):
Найдите значение выражения:
а) \(0{,}6 \sqrt{36}\);
б) \(-2{,}5 \sqrt{25}\);
в) \(\sqrt{0{,}49} + \sqrt{0{,}16}\);
г) \(\sqrt{0{,}64} - \sqrt{0{,}04}\);
д) \(-\sqrt{0{,}0036} + \sqrt{0{,}0025}\);
е) \(\sqrt{0{,}01} - \sqrt{0{,}0001}\);
ж) \(\dfrac{1}{3} \sqrt{0{,}81} - 1\);
з) \(4 - 10 \sqrt{0{,}01}\).
№296 учебника 2013-2022 (стр. 73):
Известно, что график функции \(y = \dfrac{k}{x}\) проходит через точку \(A(4;\ -0{,}5)\). Найдите \(k\) и постройте этот график.
Подсказка
№296 учебника 2023-2025 (стр. 72):
Вспомните:
- Что называют арифметическим квадратным корнем.
- Умножение десятичных дробей.
- Сложение и вычитание десятичных дробей.
- Умножение рациональных чисел.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение обыкновенных дробей.
№296 учебника 2013-2022 (стр. 73):
Вспомните:
- График обратной пропорциональности.
- Координаты точки.
- Деление и дроби.
- Деление рациональных чисел.
- Деление десятичных дробей.
- Умножение рациональных чисел.
- Умножение обыкновенных дробей.
- Умножение десятичных дробей.
- Линейное уравнение с одной переменной, его свойства.
Ответ
№296 учебника 2023-2025 (стр. 72):
а) \(0,6\sqrt{36} = 0,6\cdot6=3,6\).
б) \(-2,5\sqrt{25} = -2,5\cdot5=-12,5\).
в) \(\sqrt{0{,}49} + \sqrt{0{,}16} = 0{,}7 + 0{,}4 =\)
\(=1{,}1\)
г) \(\sqrt{0{,}64} - \sqrt{0{,}04} = 0{,}8 - 0{,}2 = 0{,}6\)
д) \(-\sqrt{0{,}0036} + \sqrt{0{,}0025} =\)
\(=-0{,}06 + 0{,}05 =-0{,}01\)
е) \(\sqrt{0{,}01} - \sqrt{0{,}0001} =\)
\(=0{,}1 - 0{,}01 = 0{,}09\)
ж) \(\dfrac{1}{3} \sqrt{0{,}81} - 1= \dfrac{1}{3} \cdot 0{,}9 - 1=\)
\(=0{,}3 - 1 = -0{,}7\)
з) \(4-10\sqrt{0{,}01} =4 - 10 \cdot 0{,}1 =\)
\(=4 - 1 = 3\)
Пояснения:
Арифметический квадратный корень из числа \(a\) — это такое неотрицательное число \(x\), при котором \(x^2 = a\).
Во всех пунктах подставляем значения переменных в выражения, производим арифметические действия, используя знание таблицы квадратов и вычисление корней.
При вычислениях учитываем то, что в записи вида \(a\sqrt b\) между числом \(a\) и \(\sqrt b\) подразумеваем знак умножения, поэтому сначала извлекаем корень, а затем выполняем умножение на число перед корнем.
№296 учебника 2013-2022 (стр. 73):
\(y = \dfrac{k}{x}\)
\(A(4;\ -0{,}5)\)
\(-0,5 = \dfrac{k}{4}\) /\(\times4\)
\(k = -2\)
\(y = -\dfrac{2}{x}\)
| \(x\) | -4 | -2 | -1 | -0,5 |
| \(y\) | 0,5 | 1 | 2 | 4 |
| \(x\) | 0,5 | 1 | 2 | 4 |
| \(y\) | -4 | -2 | -1 | -0,5 |
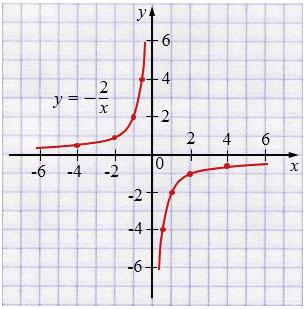
Пояснения:
Использованные правила и приёмы:
• Функция обратной пропорциональности задаётся формулой \(y=\dfrac{k}{x}\).
• Число \(k\) находим, подставляя координаты данной точки в функцию \(y=\dfrac{k}{x}\) вместо \(x\) и \(y\).
• После вычисления \(k\) записываем итоговое уравнение \(y=\frac{k}{x}\).
При решении уравнения, чтобы найти \(k\), обе части уравнения умножили на знаменатель дроби.
• Графиком обратной пропорциональности \(y=\frac{k}{x}\) является гипербола (две ветви). Строят график по точкам (для нескольких положительных и нескольких отрицательных значений \(x\) определяют значения \(y\)).
Вернуться к содержанию учебника