Упражнение 509 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

\(y = \frac{x - 4}{\sqrt{x} + 2}=\frac{(\sqrt{x})^2 - 2^2}{\sqrt{x} + 2}=\)

\(=\frac{ (\sqrt{x}-2)\cancel{(\sqrt{x}+2)}}{\cancel{\sqrt{x} + 2}}=\sqrt{x}-2\)

\(y =\sqrt{x}-2\),   \(x \ge 0\)

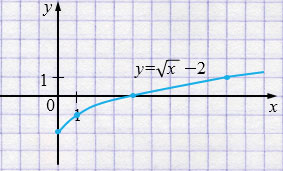
Пояснения:

Использованные приемы:

1. Применили формулу разности квадратов:

\(a^2-b^2=(a-b)(a+b)\),

учитывая свойство корня:

\((\sqrt a)^ 2 = a\).

2. Сократили дробь на \(\sqrt{x}+2\) и получили функцию \(y=\sqrt{x}-2\), графиком которой является ветвь параболы.

3. При построении графика учитываем область определения функции: корень существует только в том случае, когда подкоренное выражение неотрицательно. Строим график по точкам, учитывая область определения функции. Подбираем такие значения x, чтобы корень можно было извлечь.

а) \(15\sqrt{\frac{2}{5}} - \sqrt{160}=\)

\(=\sqrt{15^2\cdot\frac{2}{5}}- \sqrt{160}=\)

\(=\sqrt{\frac{^{45}\cancel{225}\cdot2}{\cancel5}}  - \sqrt{160}=\)

\(=\sqrt{90} - \sqrt{160}=\sqrt{9\cdot10} - \sqrt{16\cdot10}=\)

\(=3\sqrt{10} - 4\sqrt{10}=-\sqrt{10}\)

б) \(\sqrt{135} + 10\sqrt{0{,}6}=\)

\(=\sqrt{135} + \sqrt{10^2\cdot0{,}6}=\)

\(=\sqrt{135} + \sqrt{100\cdot0{,}6}=\)

\(=\sqrt{135} + \sqrt{60}=\sqrt{9\cdot15} + \sqrt{4\cdot15}=\)

\(=3\sqrt{15} + 2\sqrt{15}=5\sqrt{15}\)

в) \(6\sqrt{1\frac{1}{3}} - \sqrt{27}=\)

\(=\sqrt{^{12}\cancel{36}\cdot\frac{4}{\cancel3}} - \sqrt{27}=\)

\(=\sqrt{48} -\sqrt{27}=\sqrt{16\cdot3} -\sqrt{9\cdot3}=\)

\(=4\sqrt{3} - 3\sqrt{3}=\sqrt{3}\)

г) \(0{,}5\sqrt{24} + 10\sqrt{\frac{3}{8}}=\)

\(=\sqrt{0,5^2\cdot24} + \sqrt{10^2\cdot\frac{3}{8}}=\)

\(=\sqrt{0,25\cdot24} + \sqrt{100\cdot\frac{3}{8}}=\)

\(=\sqrt{6} + \sqrt{^{25}\cancel{100}\cdot\frac{3}{\cancel8_2}}=\)

\(=\sqrt{4\cdot1,5} + \sqrt{25\cdot1,5}=\)

\(=2\sqrt{1,5} + 5\sqrt{1,5}=7\sqrt{1,5}\)

Пояснения:

Использованные приемы:

1. Внесения множителя под знак корня:

\( k\sqrt{a} = \sqrt{k^2\,a}. \)

2. Вынесение множителя из-под знака корня:

\(\sqrt{m^2n}=m\sqrt{n}\);

3. Приведение подобных:

\(a\sqrt{b} \pm c\sqrt{b}=(a\pm c)\sqrt{b}\).