Упражнение 597 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

Пусть меньшая сторона прямоугольника равна \(x\) см, тогда вторая сторона - \(x+14\) см, диагональ \(34\).

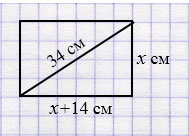
По теореме Пифагора составим уравнение:

\(x^{2}+(x+14)^{2}=34^{2}\)

\(x^{2}+x^{2}+28x+196=1156\)

\(2x^{2}+28x+196-1156=0\)

\(2x^{2}+28x-960=0\)    \(/ : 2\)

\(x^{2}+14x-480=0\)

\(a = 1\),  \(b = 14\),  \(c = -480\)

\(D=b^2 - 4ac=\)

\(=14^{2}-4\cdot1\cdot(-480)=\)

\(=196+1920=2116\);   \(\sqrt D = 46\).

\(x_{1,2} = \frac{-b\pm \sqrt D}{2a}\)

\(x_1=\frac{-14+46}{2\cdot1} =\frac{32}{2}=16\)

\(x_2=\frac{-14-46}{2\cdot1} =\frac{-60}{2}=-30\) - не удовлетворяет условию \((x>0)\).

1) \(16\) (см) - первая сторона прямоугольника.

2) \(16 + 14 = 30\) (см) - вторая сторона прямоугольника.

Ответ: \(16\) см и \(30\) см.

Пояснения:

Пояснение шагов:

1) Стороны прямоугольника образуют катеты прямоугольного треугольника с гипотенузой-диагональю, поэтому составили уравнение:

\(\;x^{2}+(x+14)^{2}=34^{2}\).

2) По формуле квадрат суммы двух выражений раскрыли скобки, привели подобные члены и получили квадратное уравнение:

\(\;x^{2}+14x-480=0\).

3) Посчитали дискриминант  и нашли корни уравнения. Отрицательный корень не подходит, так как длина стороны не может быть отрицательной. Положительный корень показывает значение длины меньшей стороны прямоугольника.

4) Находим большую сторону прямоугольника, учитывая то, что она на 14 см больше меньшей стороны.

Катеты относятся как 8 : 15. Пусть \(x\) м приходится на одну часть, тогда первый катет равен \(8x\) м, а второй - \(15x\) м. Гипотенуза равна \(6,8\) м.

По теореме Пифагора составим уравнение:

\((8x)^2 + (15x)^2 = 6,8^2\)

\(64x^2 + 225x^2 = 46,24\)

\(289x^2 = 46,24\)

\(x^2 = \frac{46,24}{289}\)

\(x^2 = 0,16\)

\(x_1 = -\sqrt{16} = -0,4\) - не удовлетворяет условию \((x>0)\).

\(x_2 = \sqrt{16} = 0,4\)

1) \(8\cdot0,4 = 3,2\) (м) - первый катет.

2) \(15\cdot0,4 = 6\) (м) - второй катет.

3) \(S=\dfrac{1}{2}\cdot3{,}2\cdot6=9{,}6\) (м²)

Ответ: площадь треугольника равна 9,6 м².

Пояснения:

Используемые приемы:

1) Катеты прямоугольного треугольника относятся как 8 : 15. Пусть \(x\) м приходится на одну часть, тогда первый катет равен \(8x\) м, а второй - \(15x\) м.

2) Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. По условию гипотенуза равна \(6{,}8\) м. Тогда можем составить следующее уравнение:

\((8x)^2 + (15x)^2 = 6,8^2\),

откуда, выполнив преобразования, получим неполное квадратное уравнение:

\(289x^2 = 46,24\).

Полученное уравнение имеет два корня:

\(x_1 = -0,4\) и \(x_2 = 0,4\).

Отрицательный корень не подходит, так как длина может быть только положительным числом.

Далее, используя положительный корень, находим катеты прямоугольного треугольника.

3) Площадь прямоугольного треугольника:

\(\displaystyle S=\frac{1}{2}ab\),

где \(a\) и \(b\) - катеты.