Упражнение 681 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№681 учебника 2023-2025 (стр. 159):
Постройте график уравнения:
а) \(y-x^{2}=0\);
б) \(y-x^{3}=0\);
в) \(0{,}5xy+1{,}5=0\);
г) \(y+x^{3}=0\).
№681 учебника 2013-2022 (стр. 154):
Один из корней уравнения \[4x^2 + bx + c = 0\] равен \(0{,}5\), а другой — свободному члену. Найдите \(b\) и \(c\).
Подсказка
№681 учебника 2023-2025 (стр. 159):
Вспомните:
№681 учебника 2013-2022 (стр. 154):
Вспомните:
- Теорему Виета.
- Свойства уравнений.
- Решение систем уравнений способом подстановки.
- Деление и дроби.
- Противоположные числа.
- Умножение обыкновенных дробей.
- Умножение десятичных дробей.
- Подобные слагаемые.
- Умножение рациональных чисел.
Ответ
№681 учебника 2023-2025 (стр. 159):
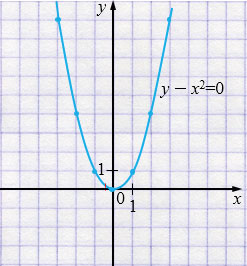
а) \(y-x^{2}=0\)
\(y=x^{2}\) - парабола.
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
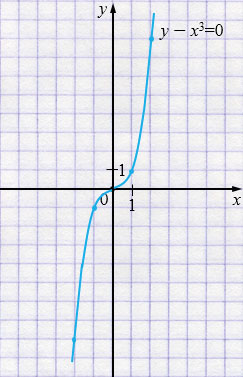
б) \(y-x^{3}=0\)
\(y=x^{3}\) - кубическая парабола.
| \(x\) | -2 | -1 | 0 | 1 | 2 |
| \(y\) | -8 | -1 | 0 | 1 | 8 |
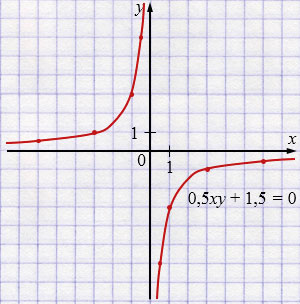
в) \(0{,}5xy+1{,}5=0\);
\(0{,}5xy=-1,5\)
\( xy=\frac{-1,5}{0,5}\)
\( xy=-3\)
\(y=-\dfrac{3}{x}\) - гипербола.
| \(x\) | -6 | -3 | -1 | -0,5 |
| \(y\) | 0,5 | 1 | 3 | 6 |
| \(x\) | 0,5 | 1 | 3 | 6 |
| \(y\) | -6 | -3 | -1 | -0,5 |
г) \(y+x^{3}=0\)
\(y=-x^{3}\). кубическая парабола.
| \(x\) | -2 | -1 | 0 | 1 | 2 |
| \(y\) | 8 | 1 | 0 | -1 | -8 |

Пояснения:
Для построения графиков сначала выражаем \(y\) через \(x\).
\(y = x^2\) - квадратичная функция, графиком которой является парабола. Строят график по точкам (для нескольких положительных и нескольких отрицательных значений \(x\) определяют значения \(y\)).
\(y = x^3\) - кубическая функция, графиком которой является кубическая парабола (возрастающая). \(y = -x^3\) - кубическая функция, графиком которой является кубическая парабола (убывающая). Строят графики по точкам (для нескольких положительных и нескольких отрицательных значений \(x\) определяют значения \(y\)).
\(y= -\frac{3}{x}\) - функция обратной пропорциональности, графиком является гипербола (две ветви, расположенные во II и VI координатных четвертях, так как \(k=-3\)). Строят график по точкам (для нескольких положительных и нескольких отрицательных значений \(x\) определяют значения \(y\)).
№681 учебника 2013-2022 (стр. 154):
\[4x^2 + bx + c = 0\]
\(a = 4\), \(b - ?\), \(c - ?\)
\(x_1 = 0{,}5\), \(x_2 = c\).
По теореме Виета:
\[ x_1 + x_2 = -\frac{b}{4}, \quad x_1 x_2 = \frac{c}{4}. \]
Составим систему уравнений:
\( \begin{cases} 0,5 + c = -\tfrac{b}{4} /\times(-4) \\ 0,5c = \frac{c}{4} /\times4 \end{cases} \)
\( \begin{cases} -2 - 4c = b \\ 2c = c \end{cases} \)
\( \begin{cases} b = -2 - 4c \\ 2c - c = 0 \end{cases} \)
\( \begin{cases} b = -2 - 4c \\ c = 0 \end{cases} \)
\( \begin{cases} b = -2 - 4\cdot0 \\ c = 0 \end{cases} \)
\( \begin{cases} b = -2 \\ c = 0 \end{cases} \)
Ответ: \(b = -2,\; c = 0.\)
Пояснения:
Мы использовали теорему Виета для суммы и произведения корней:
\[ x_1 + x_2 = -\frac{b}{a}, \quad x_1 x_2 = \frac{c}{a}. \]
По условию «один корень равен \(0{,}5\), другой равен \(c\)» подставили в формулы составили систему из двух уравнений:
Решили систему способом подстановки и получили: \(b=-2, \; c=0.\)
Вернуться к содержанию учебника