Упражнение 693 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

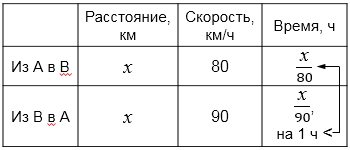
Составим уравнение:

\(\displaystyle \frac{x}{80}-\frac{x}{90}=1\)   \(/\times720\)

\(9x-8x = 720\)

\(x = 720\)

Ответ: между городами А и В 720 км.

Пояснения:

Использована формула пути:

\(S=v\cdot t\) откуда\( t=\frac{S}{v}.\)

Так как обратный путь на \(1\) час быстрее, составляем уравнение:

 \(\frac{1}{80}-\frac{1}{90}=\frac{1}{720}\).

Чтобы избавиться от знаменателей обе части уравнения домножаем на общий знаменатель дробей \(720\), получаем

\(9x-8x = 720\), откуда \(x = 720\).

Значит, расстояние между городами А и В равно 720 км.

а) \(y=2x+3\) и \(y=\dfrac{34}{x-5}\)

\(2x+3=\dfrac{34}{x-5}\)      \(/\times(x-5)\)

\((2x+3)(x-5)=34\)

\(2x^2 -10x+3x -15-34=0\)

\(2x^2-7x-49=0\)

\(a = 2\),  \(b = -7\),  \(c = -49\)

\(D = b^2-4ac=\)

\(=(-7)^2-4\cdot2\cdot(-49)=\)

\(=49+392=441,\)     \(\sqrt{D}=21.\)

\(x_1=\dfrac{-(-7) + 21}{2\cdot2}=\dfrac{28}{4}=7\).

\(x_2=\dfrac{-(-7) - 21}{2\cdot2}=\dfrac{-14}{4}=\)

\(=-\frac{7}{2}=-3,5\)

Если \(x=7\), то

\(y=2\cdot 7+3=14+3=17.\)

Если \(x=-3,5\), то

\(y=2\cdot (-3,5)+3=-7+3=-4.\)

Ответ: \((7,17), \;(-3,5,-4).\)

б) \(y=\dfrac{x^2-5x}{x+3}\) и \(y=2x\)

\(\dfrac{x^2-5x}{x+3}=2x\)      \(/\times(x+3)\)

\(x^2-5x=2x(x+3)\)

\(x^2-5x=2x^2+6x\)

\(x^2-5x-2x^2-6x=0\)

\(-x^2-11x=0\)    \(/\times(-1)\)

\(x^2+11x=0\)

\(x(x+11)=0\)

\(x=0\)   или   \(x+11=0\)

                       \(x = -11\)

Если \(x=0\), то

\(y=2\cdot 0=0.\)

Если \(x=-11\), то

\(y=2\cdot (-11)=-22.\)

Ответ: \((0,0), \;(-11,-22)\).

Пояснения:

Чтобы найти точки пересечения графиков, нужно приравнять функции и решить полученное дробное рациональное уравнение относительно \(x\). Найденные значения подставляем в одну из функций для нахождения \(y\). При этом проверяем, чтобы знаменатель не был равен нулю.

Алгоритм решения уравнений:

1) найти ОДЗ (область допустимых значений), то есть те значения переменной, при которых знаменатель обращается в нуль;

2) найти общий знаменатель дробей, входящих в уравнение (предварительно, если возможно, разложить все знаменатели на множители);

3) умножить обе части уравнения на общий знаменатель;

4) решить получившееся целое уравнение;

5) исключить из его корней те, которые совпадают с ОДЗ.

Решение целых уравнений:

1) Полное квадратное уравнение \(ax^2 + bx + c=0\), которое решается через дискриминант \(D = b^2-4ac\).

– если \(D>0\), то уравнение имеет два корня:

\(x_1 =\frac{-b+\sqrt{D}}{2a}\);

\(x_2 =\frac{-b-\sqrt{D}}{2a}\).

2) Неполное квадратное уравнение вида \(ax^2 + bx = 0\) решается вынесением общего множителя за скобки \(x(ax + b) = 0\), учитывая то, что произведение равно нулю, когда хотя бы один из множителей равен нулю.

3) Линейное уравнение вида \(ax = b\), которое при \(a\neq0\) имеет единственный корень \(x = \frac{a}{b}\).