Упражнение 692 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№692 учебника 2023-2025 (стр. 162):
В системе двух уравнений с двумя переменными первым является уравнение: \(y-\lvert x\rvert=0\) (то есть \(y=\lvert x\rvert\)); а вторым - уравнение вида \(y=kx+b\), где \(k\) и \(b\) — некоторые числа. Известно, что прямая - график второго уравнения пересекает ось \(x\) в точке \((-3;0)\). Подберите коэффициенты \(k\) и \(b\) так, чтобы система имела: 1) два решения; 2) одно решение; 3) не имела решений.
№692 учебника 2013-2022 (стр. 155):
При каком значении \(x\):
а) значение функции \(y=\dfrac{5x-7}{x^2+1}\) равно \(-6; 0; 0,8; 0,56\);
б) значение функции \(y=\dfrac{x^2-2x+6}{x+4}\) равно \(1,5; 3; 7\)?
Подсказка
№692 учебника 2023-2025 (стр. 162):
Вспомните:
- Графической способ решения систему уравнений.
- Модуль числа.
- Линейную функцию, ее график.
- Координаты точки.
- Параллельные прямые.
- Умножение рациональных чисел.
- Умножение обыкновенных дробей.
- Уравнения с двумя переменными, его свойства.
№692 учебника 2013-2022 (стр. 155):
Вспомните.
- Что называют функцией.
- Решение дробных рациональных уравнений.
- Рациональные дроби.
- Основное свойство рациональной дроби.
- Решение полных квадратных уравнений (дискриминант).
- Решение неполных квадратных уравнений.
- Что называют арифметическим квадратным корнем.
- Степень с натуральным показателем.
- Разложение многочленов на множители.
- Распределительное свойство умножения.
- Подобные слагаемые.
- Свойства уравнений.
- Линейное уравнение с одной переменной.
- Умножение рациональных чисел.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Деление рациональных чисел.
- Деление и дроби.
- Десятичная запись дробных чисел.
- Сокращение дробей.
- Неправильные дроби.
- Смешанные числа.
Ответ
№692 учебника 2023-2025 (стр. 162):
\(\begin{cases}y - |x|=0,\\ y=kx+b\end{cases}\)
\(\begin{cases}y = |x|,\\ y=kx+b\end{cases}\)
\(y=|x|\)
Если \(x\ge0\), то \(y=x\)
| \(x\) | 0 | 3 |
| \(y\) | 0 | 3 |
Если \(x<0\), то \(y=-x\)
| \(x\) | -1 | -3 |
| \(y\) | 1 | 3 |
\(y=kx+b\) пересекает ось \(x\) в точке \((-3;0)\):
\(0=k\cdot(-3)+b\)
\(0=-3k+b\)
\(b=3k\), значит, прямая
\(y=kx+3k\)
1) Система имеет 2 решения при
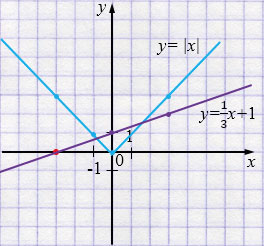
\(k = \frac13\) и \(b = 3\cdot\frac13 = 1\).
\(\begin{cases}y - |x|=0,\\ y=\frac13x+1\end{cases}\)
\(y=\frac13x+1\)
| \(x\) | 0 | 3 |
| \(y\) | 1 | 2 |
2) Система имеет одно решение при
\(k = 1\) и \(b = 3\cdot1 = 3\).
\(\begin{cases}y - |x|=0,\\ y=x+3\end{cases}\)
\(y=x+3\)
| \(x\) | 0 | 2 |
| \(y\) | 3 | 5 |

3) Система не имеет решения при
\(k=-1\) и \(b = 3\cdot(-1) = -3\)
\(\begin{cases}y - |x|=0,\\ y=-x-3\end{cases}\)
\(y=-x-3\)
| \(x\) | 0 | -2 |
| \(y\) | -3 | 1 |

Пояснения:
Количество решений системы из двух уравнений определяется количеством точек пересечения графиков этих уравнений.
Для \(y = |x|\), возможно два случая:
\(y = x\) при \(x\ge0\),
\(y = -x\) при \(x<0\).
Графиком уравнения \(y=|x|\) являются биссектрисы I и II координатных четвертей, следовательно, система из двух уравнений \(y=|x|\) и \(y = kx +b\) будет иметь:
- два решения, если прямая
\(y = kx +b\) будет пересекать каждую из биссектрис,
- одно решение, если прямая
\(y = kx +b\) будет пересекать одну из биссектрис,
- ни одного решения, если прямая
\(y = kx +b\) не будет пересекать ни одну из биссектрис.
При этом учитываем то, что если для двух уравнений системы, приведенных к виду \(y=kx+b\):
\(1)\;k_1\ne k_2\) — прямые пересекаются, система имеет одно решение.
\(2)\;k_1=k_2,\;b_1\ne b_2\) — прямые параллельны, система не имеет решений.
\(3)\;k_1=k_2,\;b_1=b_2\) — прямые совпадают, система имеет бесконечно много решений.
№692 учебника 2013-2022 (стр. 155):
а) \(y=\dfrac{5x-7}{x^2+1}\)
\(x\) - любое число.
1) \(y=-6\):
\(\dfrac{5x-7}{x^2+1}=-6\) \(/\times(x^2+1)\)
\(5x-7=-6(x^2+1)\)
\(5x-7=-6x^2-6\)
\(5x-7+6x^2+6=0\)
\(6x^2+5x-1=0\)
\(a = 6\), \(b = 5\), \(c = -1\)
\(D=b^2 - 4ac=5^2-4\cdot 6 \cdot (-1)=\)
\(=25+24=49,\) \(\sqrt D = 7\).
\(x_1=\dfrac{-5 + 7}{2\cdot6} =\dfrac{2}{12}=\dfrac{1}{6}\).
\(x_2=\dfrac{-5 - 7}{2\cdot6} =\dfrac{-12}{12}=-1\).
Ответ: при \(x_1 = \frac16\) и \(x_2 = -1\).
2) \(y=0\):
\(\dfrac{5x-7}{x^2+1}=0 \) \(/\times(x^2+1)\)
\(5x-7=0\)
\(5x=7\)
\(x=\frac{7}{5}\)
\(x = 1,4\)
Ответ: \(x = 1,4\).
3) \(y=0,8=\frac{4}{5}\):
\(\dfrac{5x-7}{x^2+1}=\frac{4}{5}\) \(/\times5(x^2+1)\)
\(5(5x - 7) = 4(x^2 + 1)\)
\(25x-35=4x^2+4\)
\(25x-35-4x^2-4=0\)
\(-4x^2 +25x - 39 = 0\) \(/\times(-1)\)
\(4x^2-25x+39=0\)
\(a = 4\), \(b = -25\), \(c = 39\)
\(D=b^2 - 4ac= (-25)^2 - 4\cdot4\cdot39 =\)
\(=625-624=1,\) \(\sqrt D = 1\).
\(x_1=\dfrac{-(-25) + 1}{2\cdot4}=\frac{26}{8}=\frac{13}{4}=3\frac{1}{4}\).
\(x_2=\dfrac{-(-25) - 1}{2\cdot4}=\frac{24}{8}=3\).
Ответ: при \(x_1 = 3\frac{1}{4}\) и \(x_2 =3\).
4) \(y=0,56=\frac{56}{100}=\frac{14}{25}\):
\(\dfrac{5x-7}{x^2+1}=\frac{14}{25}\) \(/\times25(x^2+1)\)
\(25(5x - 7) = 14(x^2 + 1)\)
\(125x-175=14x^2+14\)
\(125x-175-14x^2-14=0\)
\(-14x^2+125x -189=0\) \(/\times(-1)\)
\(14x^2-125x+189=0\)
\(a = 14\), \(b = -125\), \(c = 189\)
\(D=b^2 - 4ac=\)
\(=(-125)^2 - 4\cdot14\cdot189 =\)
\(=15625-10584=5041,\)
\(\sqrt{D}=71.\)
\(x_1=\dfrac{-(-125) + 71}{28}=\frac{196}{28}=7\).
\(x_2=\dfrac{-(-125) + 71}{28}=\frac{27}{14}=1\frac{13}{14}\).
Ответ: при \( x_1=7\) и \(x_2=1\frac{13}{14}.\)
б) \(y=\dfrac{x^2-2x+6}{x+4}\), \(x\neq-4\).
1) \(y=1,5=\frac{3}{2}\):
\(\dfrac{x^2-2x+6}{x+4}=\frac{3}{2}\) \(/\times2(x+4)\)
\(2(x^2-2x+6)=3(x+4)\)
\(2x^2-4x+12=3x+12\)
\(2x^2-4x+12-3x-12=0\)
\(2x^2-7x=0\)
\(x(2x-7)=0\)
\(x=0 \) или \(2x-7=0\)
\(2x=7\)
\( x=\frac{7}{2}\)
\(x=3,5\)
Ответ: при \(x = 0\) или \(x = 3,5\).
2) \(y=3\):
\(\dfrac{x^2-2x+6}{x+4}=3\) \(/\times(x+4)\)
\(x^2-2x+6=3(x+4)\)
\(x^2-2x+6=3x+12\)
\(x^2-2x+6-3x-12=0\)
\(x^2-5x-6=0\)
\(a = 1\), \(b = -5\), \(c = -6\)
\(D=b^2 - 4ac=\)
\((-5)^2 -4\cdot1\cdot(-6)=\)
\(=25+24 =49\), \(\sqrt D = 7\).
\(x_1=\dfrac{-(-5)+ 7}{2\cdot1}=\frac{12}{2}=6\).
\(x_2=\dfrac{-(-5)- 7}{2\cdot1}=\frac{-2}{2}=-1\).
Ответ: при \(x_1 = 6\) и \(x_2 = -1\).
3) \(y=7\):
\(\dfrac{x^2-2x+6}{x+4}=7\) \(/\times(x+4)\)
\(x^2-2x+6=7(x+4)\)
\(x^2-2x+6=7x+28\)
\(x^2-2x+6-7x-28=0\)
\(x^2-9x-22=0\)
\(a = 1\), \(b = -9\), \(c = -22\)
\(D=b^2 - 4ac=\)
\(=(-9)^2 - 4\cdot1\cdot(-22)=\)
\(D=81+88=169,\) \(\sqrt{D}=13.\)
\(x_1=\dfrac{-(-9) + 13}{2\cdot1}=\dfrac{22}{2}=11\).
\(x_2=\dfrac{-(-9) - 13}{2\cdot1}=\dfrac{-4}{2}=-2\).
Ответ: при \(x_1=11\) и \(x_2 = -2.\)
Пояснения:
Чтобы найти \(x\), при котором функция принимает данное значение \(y\), нужно в эту функцию вместо \(y\) подставить заданное значение и решить полученное дробное рациональное уравнение.
Алгоритм решения дробных рациональных уравнений:
1) найти ОДЗ (область допустимых значений), то есть те значения переменной, при которых знаменатель обращается в нуль;
2) найти общий знаменатель дробей, входящих в уравнение (предварительно, если возможно, разложить все знаменатели на множители);
3) умножить обе части уравнения на общий знаменатель;
4) решить получившееся целое уравнение;
5) исключить из его корней те, которые совпадают с ОДЗ.
Решение целых уравнений:
1) Полное квадратное уравнение \(ax^2 + bx + c=0\), которое решается через дискриминант \(D = b^2-4ac\).
– если \(D>0\), то уравнение имеет два корня:
\(x_1 =\frac{-b+\sqrt{D}}{2a}\);
\(x_2 =\frac{-b-\sqrt{D}}{2a}\).
2) Неполное квадратное уравнение вида \(ax^2 + bx = 0\) решается вынесением общего множителя за скобки \(x(ax + b) = 0\), учитывая то, что произведение равно нулю, когда хотя бы один из множителей равен нулю.
3) Линейное уравнение вида \(ax = b\), которое при \(a\neq0\) имеет единственный корень \(x = \frac{a}{b}\).
Вернуться к содержанию учебника