Упражнение 709 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№709 учебника 2023-2025 (стр. 168):
Решите систему уравнений:
\(\begin{cases} y = 0,5x^2 - 2, \\ y - x = 2 \end{cases}\)
сначала графическим способом, а затем аналитическим.
№709 учебника 2013-2022 (стр. 158):
Автобус проехал расстояние между пунктами \(A\) и \(B\), равное 400 км, с некоторой постоянной скоростью. Возвращаясь обратно, он 2 ч ехал с той же скоростью, а затем увеличил скорость на 10 км/ч и возвратился в пункт \(A\), затратив на обратный путь на 20 мин меньше, чем на путь из \(A\) в \(B\). Сколько времени затратил автобус на обратный путь?
Подсказка
№709 учебника 2023-2025 (стр. 168):
Вспомните:
- Графический способ решения систем уравнений.
- Метод подстановки при решении систем уравнений.
- Уравнение с двумя переменными, их свойства.
- График квадратичной функции.
- Линейная функция, ее график.
- Полные квадратные уравнения.
- Степень с натуральным показателем.
- Деление и дроби.
- Умножение рациональных чисел.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Деление рациональных чисел.
- Подобные слагаемые.
- Арифметический квадратный корень.
№709 учебника 2013-2022 (стр. 158):
Вспомните.
- Задачи на движение.
- Решение дробных рациональных уравнений.
- Рациональные дроби.
- Основное свойство рациональной дроби.
- Полные квадратные уравнения (дискриминант).
- Арифметический квадратный корень.
- Подобные слагаемые.
- Свойства уравнений.
- Умножение одночлена на многочлен.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение рациональных чисел.
- Деление рациональных чисел.
- Деление и дроби.
- Неправильные дроби.
- Смешанные числа.
Ответ
№709 учебника 2023-2025 (стр. 168):
\(\begin{cases} y = 0,5x^2 - 2, \\ y - x = 2 \end{cases}\)
\(\begin{cases} y = 0,5x^2 - 2, \\ y = x+2 \end{cases}\)
1) Графический способ:
\(y=0,5x^2-2\) - парабола.
| \(x\) | -4 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | 6 | 0 | -1,5 | -2 | -1,5 | 0 | 6 |
\(y = x+2\) - прямая.
| \(x\) | 0 | 2 |
| \(y\) | 2 | 4 |
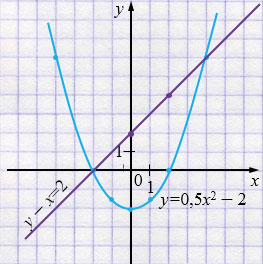
2) Аналитический способ:
\(\begin{cases} x+2 = 0,5x^2 - 2, \\ y = x+2 \end{cases}\)
\( x+2=0,5x^2-2 \)
\( 0,5x^2 - x - 2-2 = 0 \)
\( 0,5x^2 - x - 4 = 0 \) \(/\times2\)
\( x^2 - 2x - 8 = 0 \)
\(a = 1\), \(b = -2\), \(c = -8\)
\(D =b^2 - 4ac =\)
\(=(-2)^2 - 4\cdot1\cdot(-8)=\)
\(=4 + 32 = 36\), \(\sqrt D = 6\).
\(x_{1,2} = \frac{-b\pm \sqrt D}{2a}\)
\( x_1 = \frac{(-(-2) + 6}{2\cdot1} = \frac{8}{2} = 4\).
\( x_1 = \frac{(-(-2) - 6}{2\cdot1} = \frac{-4}{2} = -2\).
\(y_1 = 4 + 2 = 6\).
\(y_2 = -2 + 2 = 0\)
Ответ: \((4;6)\), \((-2;0)\).
Пояснения:
Суть графического метода решения системы уравнений с двумя переменными:
1) построить на одной координатной плоскости графики уравнений, входящих в систему;
2) найти координаты всех точек пересечения построенных графиков;
3) полученные пары чисел и будут искомыми решениями.
В качестве аналитического способа используем метод подстановки:
1) выражают из уравнения первой степени одну переменную через другую;
2) подставляют полученное выражение в уравнение второй степени, в результате чего приходят к уравнению с одной переменной;
3) решают получившиеся уравнение с одной переменной;
4) находят соответствующие значения второй переменной.
№709 учебника 2013-2022 (стр. 158):

\(20 \; мин = \frac{20}{60} \; ч = \frac13 \; ч\)
Составим уравнение:
\(2 + \frac13 + \frac{400 - 2x}{x + 10} = \frac{400}{x}\)
\(2\frac13 + \frac{400 - 2x}{x + 10}=\frac{400}{x}\)
\(\frac73 + \frac{400 - 2x}{x + 10}=\frac{400}{x}\) \(/\times 3x(x+10)\)
ОДЗ: \(x\neq0\) и \(x + 10\neq 0\)
\(x\neq-10\)
\(7x(x+10)+3x(400-2x) =1200(x+10)\)
\(7x^2 + 70x +1200x - 6x^2 = 1200x +12 000\)
\(7x^2 + 70x +\cancel{1200x} - 6x^2 - \cancel{1200x} -12 000=0\)
\( x^2 + 70x - 12000 = 0\)
\(a = 1\), \(b = 70\), \(c = -12000\)
\(D = b^2 - 4ac =\)
\(=70^2 - 4 \cdot 1 \cdot (-12000) =\)
\(=4900 + 48000 = 52900\),
\(\sqrt{D} = 230.\)
\( x_1 = \frac{-70 + 230}{2\cdot1}=\frac{160}{2}= 80\).
\( x_2 = \frac{-70 - 230}{2\cdot1}=\frac{-300}{2} = -150\) - не удовлетворяет условию.
1) \(80\) (км/ч) - скорость из А в В.
2) \(\frac{400}{80} = 5\) (ч) - время на путь из А в В.
3) \(5 \; ч - 20 \; мин = 4 \; ч\; 40 \;мин\) - время на путь из В в А.
Ответ: на обратный путь автобус затратил 4 ч 40 мин.
Пояснения:
Время в пути вычисляется по формуле \[t=\frac{S}{v}.\]
Мы обозначили скорость автобуса при движении из А в В за \(x\). Используя условия задачи (движение с разными скоростями и разница во времени), составили дробное рациональное уравнение:
\(2 + \frac13 + \frac{400 - 2x}{x + 10} = \frac{400}{x}\).
Алгоритм решения дробного рационального уравнений:
1) найти ОДЗ (область допустимых значений), то есть те значения переменной, при которых знаменатель обращается в нуль;
2) найти общий знаменатель дробей, входящих в уравнение;
3) умножить обе части уравнения на общий знаменатель;
4) решить получившееся целое уравнение;
5) исключить из его корней те, которые совпадают с ОДЗ.
После того как обе части уравнения домножили на общий знаменатель и выполнили преобразования, получили квадратное уравнение, у которого дискриминант \(D = b^2 - 4ac>0\), поэтому уравнение имеет два корня: \(80\) и \(-150\). Но отрицательный корень не подходит, так как скорость может быть только положительным числом. Значит, скорость автобуса при движении из А в В равна 80 км/ч. Тогда время на путь из А в В:
\(\frac{400}{80} = 5\) (ч).
На обратный путь (из В в А) автобус затратил на 20 мин меньше, значит, на обратный путь автобус затратил:
\(5 \; ч - 20 \; мин = 4 \; ч\; 40 \;мин\).
Вернуться к содержанию учебника