Упражнение 718 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№718 учебника 2023-2025 (стр. 169):
При каких значениях \(x\):
а) трёхчлен \(-x^2-2x+168\) принимает положительные значения;
б) трёхчлен \(15x^2+x-2\) принимает отрицательные значения;
в) дробь \(\dfrac{x+14}{3-2x}\) принимает отрицательные значения;
г) дробь \(\dfrac{6-5x}{x+25}\) принимает положительные значения?
№718 учебника 2013-2022 (стр. 159):
Сплав меди с цинком, содержащий 6 кг цинка, сплавили с 13 кг цинка. В результате содержание меди в сплаве понизилось на 26%. Какова была первоначальная масса сплава?
Подсказка
№718 учебника 2023-2025 (стр. 169):
Вспомните:
- Разложение квадратного трехчлена на множители.
- Умножение рациональных чисел.
- Деление рациональных чисел.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Деление и дроби.
- Десятичная запись дробных чисел.
- Сравнение рациональных чисел.
№718 учебника 2013-2022 (стр. 159):
Вспомните.
- Решение дробных рациональных уравнений.
- Рациональные дроби.
- Основное свойство рациональной дроби.
- Полные квадратные уравнения (дискриминант).
- Арифметический квадратный корень.
- Подобные слагаемые.
- Свойства уравнений.
- Умножение одночлена на многочлен.
- Умножение многочлена на многочлен.
- Противоположные числа.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Деление рациональных чисел.
- Деление и дроби.
Ответ
№718 учебника 2023-2025 (стр. 169):
а) \( -x^2-2x+168>0 \)
\( -x^2-2x+168=0 \) \(/\times(-1)\)
\(x^2+2x-168=0 \)
\(a = 1\), \(b = 2\), \(c = -168\)
\(D=b^2 - 4ac=\)
\(=2^2-4\cdot1\cdot(-168)=\)
\(=4+672=676\), \(\sqrt{D}=26 \)
\(x=\frac{-b\pm\sqrt D}{2a}\)
\( x_1=\frac{-2+26}{2\cdot1}=\frac{24}{2} = 12\)
\( x_2=\frac{-2-26}{2\cdot1}=\frac{-28}{2} = -14\)
\( -x^2-2x+168=-(x-12)(x+14) \)
\(-(x-12)(x+14)>0 \)
1) \( \begin{cases} x-12>0, \\ x+14<0\end{cases} \)
2) \( \begin{cases} x-12<0, \\ x+14>0\end{cases} \)
\(-14 < x < 12\)
Ответ: при \(-14 < x < 12\).
б) \( 15x^2+x-2<0 \)
\( 15x^2+x-2=0 \)
\(a = 15\), \(b = 1\), \(c = -2\)
\(D=b^2 - 4ac=1^2-4\cdot15\cdot(-2)=\)
\(=1+120=121\), \( \sqrt{D}=11 \)
\(x=\frac{-b\pm\sqrt D}{2a}\)
\( x_1=\frac{-1+11}{2\cdot15}=\frac{10}{30} = \frac13\)
\( x_2=\frac{-1-11}{2\cdot15}=\frac{-12}{30} = -\frac25\)
\( 15x^2+x-2=15(x-\frac13)(x+\frac25)\)
\(15(x-\frac13)(x+\frac25)<0\)
1) \( \begin{cases} x-\frac13>0, \\ x+\frac25<0\end{cases} \)
2) \( \begin{cases} x-\frac13<0, \\ x+\frac25>0\end{cases} \)
\( \begin{cases} x<\frac13, \\ x>-\frac25\end{cases} \)
\(-\frac25 < x < \frac13\)
Ответ: при \(-\frac25 < x < \frac13\).
в) \(\dfrac{x+14}{3-2x}<0\)
ОДЗ: \(3-2x \neq 0\)
\(2x\neq3\)
\(x \neq \frac32\)
\(x \neq1,5\)
1) \( \begin{cases} x+14>0, \\ 3-2x<0\end{cases} \)
\( \begin{cases} x>-14, \\ 2x>3\end{cases} \)
\( \begin{cases} x>-14, \\ x>\frac32 \end{cases} \)
\( \begin{cases} x>-14, \\ x>1,5 \end{cases} \)
\(x > 1,5\)
2) \( \begin{cases} x+14<0, \\ 3-2x>0\end{cases} \)
\( \begin{cases} x<-14, \\ 2x<3\end{cases} \)
\( \begin{cases} x<-14, \\ x<\frac32\end{cases} \)
\( \begin{cases} x<-14, \\ x<1,5\end{cases} \)
\(x<-14\)
Ответ: \(x<-14\) или \(x>1,5\).
г) \(\dfrac{6-5x}{x+25}>0\)
ОДЗ: \(x + 25 \neq 0\)
\(x\neq-25\)
1) \( \begin{cases} 6-5x>0, \\ x+25>0\end{cases} \)
\( \begin{cases} 5x<6, \\ x>-25\end{cases} \)
\( \begin{cases} x<\frac65, \\ x>-25\end{cases} \)
\( \begin{cases} x<1,2, \\ x>-25\end{cases} \)
\(-25 < x < 1,2\)
2) \( \begin{cases} 6-5x<0, \\ x+25<0\end{cases} \)
\( \begin{cases} 5x>6, \\ x< -25\end{cases} \)
\( \begin{cases} x>\frac65, \\ x< -25\end{cases} \)
\( \begin{cases} x>1,2, \\ x< -25\end{cases} \) - решений нет.
Ответ: при \(-25 < x < 1,2\).
Пояснения:
В пунктах а) и б) квадратный трехчлен разложили на множители согласно формуле:
\(ax^2 +bx + c = a(x - x_1)(x - x_2)\),
где \(x_1\) и \(x_2\) корни трехчлена
\(ax^2 +bx + c\).
Затем учли то, что произведение отрицательно, если в нем нечетное количество отрицательных множителей, и произведение положительно, если в нем четное количество отрицательных множителей.
В пунктах в) и г) сначала определили значения, при которых дробь не имеет смысла (ОДЗ). Затем учли то, что значение дроби отрицательно, если ее числитель и знаменатель имеют разные знаки, и значение дроби положительно, если ее числитель и знаменатель имеют одинаковые знаки.
№718 учебника 2013-2022 (стр. 159):
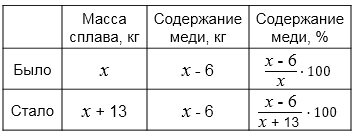
Составим уравнение:
\(\frac{x-6}{x}\cdot100 - \frac{x-6}{x + 13}\cdot100=26\) \(/\times x(x+13)\)
ОДЗ: \(x\neq0\) и \(x + 13\neq 0\)
\(x\neq-13\)
\(100(x-6)(x+13) - 100x(x-6)=26x(x+13)\)
\(100(x^2+13x -6x-78) - 100x^2 + 600 x = 26x^2 + 338x\)
\(\cancel{100x^2} + 1300x - \cancel{600x} - 7800 - \cancel{100x^2} + \cancel{600x} -26x^2 -338x = 0\)
\(-26x^2 + 962x - 7800 = 0\) \(/ : (-26)\)
\(x^2 - 37x + 300 = 0\)
\(a = 1\), \(b = -37\), \(c = 300\)
\(D = b^2 - 4ac =\)
\(=(-37)^2 - 4\cdot 1 \cdot 300 =\)
\(=1369 - 1200 = 169\), \(\sqrt D = 13\).
\(x_1 = \frac{-(-37) + 13}{2\cdot1} = \frac{50}{2} = 25\).
\(x_2 = \frac{-(-37) - 13}{2\cdot1} = \frac{24}{2} = 12\).
Ответ: первоначальная масса сплава могла быть \(12\) кг или \(25\) кг.
Пояснения:
Обозначили массу сплава за \(x\). Выразили долю меди до добавления цинка и после. Учитывая условие о том, что доля меди уменьшилась на 26%, составили дробное рациональное уравнение:
\(\frac{x-6}{x}\cdot100 - \frac{x-6}{x + 13}\cdot100=26\)
Алгоритм решения дробного рационального уравнений:
1) найти ОДЗ (область допустимых значений), то есть те значения переменной, при которых знаменатель обращается в нуль;
2) найти общий знаменатель дробей, входящих в уравнение;
3) умножить обе части уравнения на общий знаменатель;
4) решить получившееся целое уравнение;
5) исключить из его корней те, которые совпадают с ОДЗ.
После того как обе части уравнения домножили на общий знаменатель и выполнили преобразования, получили квадратное уравнение, у которого дискриминант \(D = b^2 - 4ac>0\), поэтому уравнение имеет два корня: \(25\) и \(12\). Оба корня удовлетворяют условию задачи. Значит, первоначальная масса сплава могла быть \(12\) кг или \(25\) кг.
Вернуться к содержанию учебника