Упражнение 897 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

а) \(9a + \dfrac{1}{a} \geq 6\), при \(a>0\).

\( 9a ^{\color{blue}{\backslash a}} + \frac{1}{a} - 6 ^{\color{blue}{\backslash a}} \geq 0. \)

\( \frac{9a^2 + 1 - 6a}{a} \geq 0\)

\( \frac{9a^2 - 6a + 1}{a} \geq 0\)

\( \frac{(3a - 1)^2}{a} \geq 0\) - верно, так как \(a > 0\) и \((3a - 1)^2 \geq0\) при любом \(a\).

Что и требовалось доказать.

б) \(25b + \dfrac{1}{b} \leq -10\), при \(b < 0\).

\( 25b ^{\color{blue}{\backslash b}} + \frac{1}{b} + 10 ^{\color{blue}{\backslash b}} \leq 0\)

\( \frac{25b^2 + 1 + 10b}{b} \leq 0\)

\( \frac{25b^2 + 10b + 1}{b} \leq 0\)

\( \frac{(5b +1)^2}{b} \leq 0\) - верно, так как \(b < 0\) и \((5b +1)^2 \geq0\) при любом \(b\).

Что и требовалось доказать.

Пояснения:

В каждом пункте мы свели задачу к исследованию квадратного трёхчлена.

С помощью выделения полного квадрата (\((3a-1)^2\) и \((5b+1)^2\)) показали, что числители всегда неотрицательны.

С учётом знака знаменателя получаем требуемые неравенства.

Использованные приемы и формулы:

- Квадрат разности двух выражений:

\((a - b)^2 = a^2 -2ab + b^2\).

- Квадрат суммы двух выражений:

\((a + b)^2 = a^2 + 2ab + b^2\).

- Свойство степени:

\(a^nb^n = (ab)^n\).

\[x^2 - 6bx + 9b^2 - 16 = 0\]

\(A=1,\; B=-6b,\; C=9b^2-16.\)

\(D = B^2 - 4AC =\)

\(=(-6b)^2 - 4(9b^2-16) = \)

\(=36b^2 - 36b^2 + 64 = 64>0\) - уравнение имеет 2 корня.

\(\sqrt D=8\).

\(x_1 = \dfrac{6b + 8}{2} = \dfrac{\cancel2(3b + 4)}{\cancel2}=\)

\(=3b + 4.\)

\(x_2 = \dfrac{6b - 8}{2} = \dfrac{\cancel2(3b - 4)}{\cancel2}=\)

\(=3b - 4.\)

\(\begin{cases} 3b+4 < 0,\\ 3b-4 < 0 \end{cases}\)

\(\begin{cases} 3b < -4, / : 3 \\ 3b < 4  / : 3 \end{cases}\)

\(\begin{cases} b < -\frac43, \\ b < \frac43 \end{cases}\)

\(\begin{cases} b < -1\frac13, \\ b < 1\frac13 \end{cases}\)

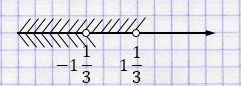
Ответ: при \(b\in(-\infty;-1\tfrac{1}{3})\) уравнение имеет два отрицательных корня.

Пояснения:

При решении учитываем то, что квадратное уравнение

\(Ax^2 + Bx + C=0\) имеет два корня в том случае, когда дискриминант

\(D = B^2-4AC > 0\), и тогда корни уравнения:

\(x_{1,2} =\frac{-B \pm \sqrt D}{2A}\).

По условию корни уравнения должны быть отрицательны. Поэтому, найдя корни уравнения \(x_1\) и \(x_2\), мы рассматриваем систему из двух неравенств относительно переменной \(b\).

Чтобы решить систему неравенств, нужно найти пересечение решений неравенств системы, то есть найти множество чисел, которое является одновременно решением и одного неравенства и решением другого неравенства. Если решения неравенств не пересекаются, то система решений не имеет.

При решении неравенств системы используем то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.