Упражнение 894 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

1) \(BO\) - медиана \(\Delta ABC\).

\(OD = BO\)

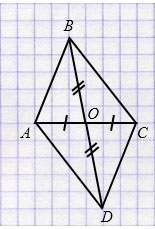
2) Четырёхугольник \(ABCD\) - параллелограмм, так как \(O\) — середина \(AC\), а отрезки \(BO\) и \(OD\) равны.

3) 1) В треугольнике \(\Delta ABD\) по неравенству треугольника:

\(BD < AD + AB.\)

\(AD = BC\) (противоположные стороны параллелограмма) и

\(BD = 2BO = 2m_b\), тогда:

\(2m_b < BC + AB\).

2) В треугольнике \(\Delta ABO\) по неравенству треугольника:

\(AB < AO + BO\).

В треугольнике \(\Delta BOC\) по неравенству треугольника:

\(BC < OC + BO\).

\(AB + BC < (AO + BO) + (OC + BO)\)

\(AB + BC < (AO + OC) + (BO + BO)\)

\(AB + BC < AC + 2BO\)

\(AB + BC < AC + 2BO\)

\(АВ + ВС < AC + 2m_b\)

\(AB + BC - AC <  2m_b\)

4) \(2m_b < BC + AB\) и

\(AB + BC - AC <  2m_b\);

\(2m_c < AC + BC\) и

\(AC + BC - AB <  2m_с\);

\(2m_a < AB + AC\) и

\(AC +  AB - BC <  2m_a\).

5) Верхняя граница:

\(2m_a + 2m_b + 2m_c < (AB + AC) + (BC + AB) + ( AC + BC)\)

\(2m_a + 2m_b + 2m_c < 2AB + 2AC + 2BC\)

\(2(m_a + m_b + m_c) < 2(AB + AC + BC)\)  \( /: 2\)

\(m_a + m_b + m_c < AB + AC + BC\)

\(m_a + m_b + m_c < P\)

\(P =AB + AC + BC\) - периметр \(\Delta ABC\).

Нижняя граница:

\((AC + AB -BC)+(AB + BC - AC) + (AC + BC - AB) <  2m_a + 2m_b + 2m_c\)

\(\cancel{AC} + \cancel{AB} - \cancel{BC}+AB + BC - \cancel{AC} + AC + \cancel{BC} - \cancel{AB} <  2m_a + 2m_b + 2m_c\)

\(AB + BC + AC < 2(m_a + m_b + m_c)\) \( /: 2\)

\(\frac12(AB + BC + AC) < m_a + m_b + m_c\)

\(\frac12P < m_a + m_b + m_c\)

Ответ:

\(\frac12P < m_a + m_b + m_c < P\).

Пояснения:

Медиана треугольника - это отрезок, который соединяет вершину треугольника с серединой противоположной стороны.

Учли то, что четырехугольник, у которого диагонали точкой пересечения делятся пополам, является параллелограммом.

Использовали свойство параллелограмма: противоположные стороны параллелограмма равны.

Неравенство треугольника: сумма длин двух сторон треугольника больше длины третьей стороны.

Свойства неравенств:

- если почленно сложить верные неравенства одного знака, то получится верное неравенство;

- если части неравенства умножить или разделить на одно и то же положительное число, знак неравенства сохраняется;

- если к частям неравенства прибавить или вычесть одно и то же число, знак неравенства сохраняется.

При оценке суммы медиан треугольника получили, что сумма медиан треугольника меньше периметра этого треугольника, но больше полупериметра этого треугольника.

а) \(-1 \le 15x+14 < 44 \)

\(\begin{cases} 15x+14 \ge -1,\\ 15x+14 < 44 \end{cases} \)

\(\begin{cases} 15x \ge -1 - 14,\\ 15x < 44 - 14 \end{cases} \)

\(\begin{cases} 15x \ge -15,   / : 15 \\ 15x < 30    / : 15 \end{cases} \)

\(\begin{cases} x \ge -1, \\ x < 2 \end{cases} \)

Ответ: \([-1,\,2)\).

б) \(-1 \le \dfrac{6-a}{3} \le 1 \)

\(\begin{cases} \dfrac{6-a}{3} \ge -1, /\times3 \\ \dfrac{6-a}{3} \le 1  /\times3 \end{cases} \)

\(\begin{cases} 6 - a \ge -3, \\ 6-a \le 3 \end{cases} \)

\(\begin{cases} -a \ge -3 - 6, \\ -a \le 3-6 \end{cases} \)

\(\begin{cases} -a \ge -9, /\times(-1) \\ -a \le -3   / \times (-1) \end{cases} \)

\(\begin{cases} a \le 9, \\ a \ge 3 \end{cases} \)

Ответ: \([3,\,9]\).

в) \(-1{,}2 < 1-2y < 2{,}4 \)

\(\begin{cases} 1-2y > -1,2,\\ 1-2y < 2{,}4 \end{cases} \)

\(\begin{cases} -2y > -1,2 - 1,\\ -2y < 2{,}4 - 1 \end{cases} \)

\(\begin{cases} -2y > -2,2,    / : (-2) \\ -2y < 1{,}4     / : (-2) \end{cases} \)

\(\begin{cases} y < 1,1, \\ y > -0,7 \end{cases} \)

Ответ: \((-0{,}7,\,1{,}1)\).

г) \(-2 < \dfrac{4x-1}{3} \le 0 \)

\(\begin{cases} \dfrac{4x-1}{3} > -2,  /\times3 \\ \dfrac{4x-1}{3} \le 0   /\times3 \end{cases}\)

\(\begin{cases} 4x-1 > -6, \\ 4x-1 \le 0 \end{cases}\)

\(\begin{cases} 4x > -6+1, \\ 4x \le 1 \end{cases}\)

\(\begin{cases} 4x > -5,  / : 4 \\ 4x \le 1  / : 4 \end{cases}\)

\(\begin{cases} x > -1,25, \\ x \le 0,25 \end{cases}\)

Ответ: \(\left(-1,25,\,0,25\right]\).

Пояснения:

Двойное неравенство удобно раскладывать на систему из двух простых неравенств:

1) средняя часть больше левой части;

2) средняя часть меньше правой.

Чтобы решить систему неравенств, нужно найти пересечение решений неравенств системы, то есть найти множество чисел, которое является одновременно решением и одного неравенства и решением другого неравенства. Если решения неравенств не пересекаются, то система решений не имеет.

При решении неравенств системы используем то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство.

- если обе части неравенства разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.