Упражнение 959 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

а) \(\dfrac{\sqrt{7-14x}}{x+8}\)

1) \(7 - 14x \geqslant 0\)

\(-14x \geqslant -7\)   \(/ : (-14)\)

\(x \leqslant \dfrac{7}{14}\)

\(x \leqslant \dfrac{1}{2}\)

\(x \leqslant 0,5\)

2) \(x+8 \neq 0\)

\(x \neq -8\).

Ответ: \(x \in (-\infty; -8)\cup (-8; 0,5]\).

б) \(\dfrac{6}{\sqrt{4-x}-1}\)

1) \(4 - x \geqslant 0\)

\(x\leqslant 4\)

2) \(\sqrt{4-x}-1 \neq 0\)

\(\sqrt{4-x} \neq 1\)

\(4 - x \neq 1\)

\(-x \neq 1 - 4\)

\(-x\neq-3\)

\(x \neq3\)

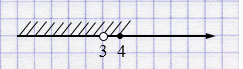
Ответ: \(x \in (-\infty; 3)\cup (3; 4]\).

Пояснения:

При нахождении области определения функций, нужно учитывать то, что:

— подкоренное выражение должно быть неотрицательным (\(\geqslant 0\));

— знаменатель должен быть отличен от нуля.

Составляем неравенства относительно подкоренных выражений. При решении неравенств используем то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

Точку, в которой знаменатель не равен нулю, на координатной прямой делаем "выколотой" (незакрашенной), так как в этой точке функция не существует и, записывая промежутки, около этой точки ставим круглую скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.

а) \(\begin {cases} \dfrac{5y-1}{6}-\dfrac{2y-1}{2}>0,  /\times6 \\[4pt]1-\dfrac{y+4}{3}<0   /\times3\end {cases} \)

\(\begin {cases} 5y-1-3(2y-1)>0, \\[4pt]3-(y+4)<0 \end {cases} \)

\(\begin {cases} 5y-1-6y+3>0, \\[4pt]3-y-4<0 \end {cases} \)

\(\begin {cases} -y + 2 >0, \\[4pt]-y-1<0 \end {cases} \)

\(\begin {cases} -y >-2, /\times(-1) \\[4pt]-y<1   /\times(-1) \end {cases} \)

\(\begin {cases} y <2, \\[4pt]y>-1   \end {cases} \)

\(y \in (-1; 2)\)

Ответ: отрицательные значения при \(y \in (-1; 0)\)

б) \(\begin {cases} (y+6)(5-y)+y(y-1)>0,\\[2pt]0{,}3y(10y+20)-3y^{2}+30>0 \end {cases} \)

\(\begin {cases} 5y - \cancel{y^2}+30 - 6y+ \cancel{y^2} - y>0,\\[2pt] \cancel{3y^2} + 6y - \cancel{3y^2} + 30 >0 \end {cases} \)

\(\begin {cases} -2y +30>0,\\[2pt] 6y+ 30 >0 \end {cases} \)

\(\begin {cases} -2y > -30,  / : (-2) \\[2pt] y > -30 / : 6\end {cases} \)

\(\begin {cases} y < 15, \\[2pt] y > -5 \end {cases} \)

\(y \in (-5; 15)\)

Ответ: отрицательные значения при \(y \in (-5; 0)\).

Пояснения:

Чтобы найти отрицательные значения \(y\), удовлетворяющие системе неравенств, нужно решить эту систему и из решения системы выбрать отрицательные значения \(y\).

Чтобы решить систему неравенств, нужно найти пересечение решений неравенств системы, то есть найти множество чисел, которое является одновременно решением и одного неравенства и решением другого неравенства. Если решения неравенств не пересекаются, то система решений не имеет.

При решении систем неравенств, сначала, если необходимо, избавляемся от знаменателей, домножив обе части неравенства на общий знаменатель всех дробей, входящих в него, затем раскрываем скобки, используя распределительное свойство умножения, при этом используем свойства неравенств:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.