Упражнение 1130 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1130 учебника 2023-2025 (стр. 254):
Дана функция \( f(x) = \sqrt{x} \). Укажите значения аргумента \( x \), при которых выполняется условие:
а) \( f(x) > 10 \);
б) \( 3 < f(x) < 5 \).
Проиллюстрируйте свой ответ на графике.
№1130 учебника 2013-2022 (стр. 256):
Из города M в город N вышел автобус со скоростью 40 км/ч. Через четверть часа он встретил ехавшую из города N легковую автомашину. Эта машина доехала до города M, через 15 минут выехала обратно в город N и обогнала автобус в 20 км от города N. Найдите расстояние между городами M и N, если скорость легковой машины 50 км/ч.
Подсказка
№1130 учебника 2023-2025 (стр. 254):
Вспомните:
- График функции квадратного корня (\(y = \sqrt x\)).
- Арифметический квадратный корень.
- Координаты точки.
- Числовые промежутки.
№1130 учебника 2013-2022 (стр. 256):
Вспомните:
- Задачи на движение.
- Решение задач с помощью уравнений.
- Линейное уравнение с одной переменной.
- Единицы измерения времени.
- Умножение обыкновенных дробей.
- Сокращение дробей.
- Распределительное свойство умножения.
- Подобные слагаемые.
- Деление и дроби.
Ответ
№1130 учебника 2023-2025 (стр. 254):
а) \( f(x) > 10 \)
\[ \sqrt{x} > 10 \]
\[ x > 100 \]
| \(x\) | 0 | 9 | 25 | 100 |
| \(y\) | 0 | 3 | 5 | 10 |
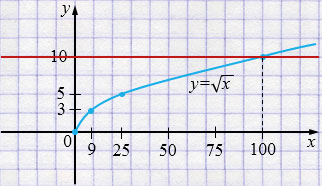
Ответ: при \( x > 100 \) функция \( f(x) > 10 \).
б) \( 3 < f(x) < 5 \)
\[ 3 < \sqrt{x} < 5 \]
\[ 9 < x < 25 \]
| \(x\) | 0 | 9 | 25 | 100 |
| \(y\) | 0 | 3 | 5 | 10 |
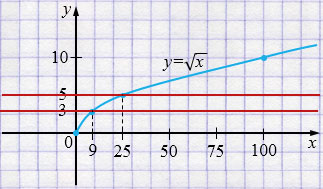
Ответ: при \( 9 < x < 25 \) функция \( 3 < f(x) < 5 \)
Пояснения:
Функция \( f(x) = \sqrt{x} \) определена при \( x \ge 0 \) и является возрастающей, то есть при увеличении \( x \) увеличивается и значение функции.
Чтобы решить неравенства, заменяем \( f(x) \) на \( \sqrt{x} \) и возводим части в квадрат (так как обе стороны неотрицательные).
Таким образом, неравенства с функцией \( \sqrt{x} \) превращаются в неравенства относительно \( x \):
1) \( \sqrt{x} > a \), откуда \(x > a^2\),
2) \( \sqrt{x} < b \), откуда \( x < b^2. \)
Поэтому:
\( f(x) > 10 \) при \(x > 100, \)
\( 3 < f(x) < 5 \) при \( 9 < x < 25. \)
№1130 учебника 2013-2022 (стр. 256):
Скорость автобуса - \(40\) км/ч.
Скорость машины - \(50\) км/ч.
Время в пути автобуса до встречи с машиной:
\(15\) мин = \(\frac{15}{60} \) ч = \(\frac14\) ч.
Расстояние между М и N - \(x\) км.
1) \(40 \cdot \frac14 = 10 \) (км) - расстояние от М до первой встречи автобуса и машины.
2) \(10 : 50 = \frac15\) (ч) - время, которое затратила машина на путь от места первой встречи до города М.
3) \(\frac{x - 10 - 20}{40} = \frac{x - 30}{40}\) (ч) - время, которое затратил автобус на путь от первой встречи с машиной до второй.
4) \(\frac15 + \frac14 + \frac{x - 20}{50}\) (ч) - время, которое затратила машина на путь от первой встречи с автобусом до второй.
5) Составим уравнение:
\(\frac{x - 30}{40} = \frac15 + \frac14 + \frac{x - 20}{50}\) \(/\times200\)
\(5(x-30)=40 + 50+4(x-20)\)
\(5x - 150 = 90 + 4x - 80\)
\(5x - 4x = 10 + 150\)
\(x = 160\)
Ответ: расстояние между городами M и N равно \(160\) км.
Пояснения:
Решаем задачу с помощью уравнения, обозначив расстояние между городами М и N через \(x\) и учитывая то, что время в пути с момента первой встречи до второй встречи у машины и автобуса одинаковое.
К моменту первой встречи автобус проехал 10 км, двигаясь из М в N, а к моменту второй встречи автобусу осталось проехать 20 км до пункта N, Значит, учитывая то, что скорость автобуса 40 км/ч, время между встречами:
\(\frac{x - 10 - 20}{40} = \frac{x - 30}{40}\) (ч).
После первой встречи с автобусом машина проехала 10 км до города М, через 15 минут выехала обратно в город N и обогнала автобус в 20 км от города N. Значит, учитывая то, что скорость машины 50 км/ч, время между встречами:
\(\frac15 + \frac14 + \frac{x - 20}{50}\) (ч).
Время между встречами для автобуса и машины одинаковое, поэтому можем составить следующее уравнение:
\(\frac{x - 30}{40} = \frac15 + \frac14 + \frac{x - 20}{50}\).
При решении уравнения сначала избавляемся от знаменателей, домножив обе части уравнения на общий знаменатель всех дробей, входящих в уравнение. Затем все компоненты с переменной переносим в левую сторону, а без переменной - в правую, изменив их знаки на противоположные, и выражаем переменную. Получили \(x = 160\), значит, расстояние между городами M и N равно \(160\) км.
Вернуться к содержанию учебника