Упражнение 192 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 69

\(y=-0{,}25x^{2}\) - парабола, ветви которой направлены вниз.

 \(x\in[-6;\,2]\)

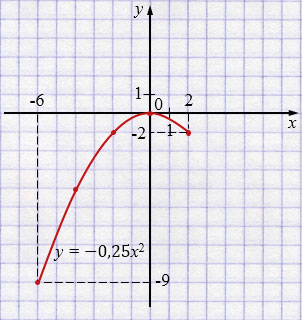
\( y_{\text{наиб.}}=0\) при \( x=0\).

\( y_{\text{наим.}}=-9\) при \( x=-6\).

Пояснения:

При построении графика функции берем значения \(x\) из промежутка \([-6;\,2]\), включая его концы, то есть составляем таблицу для  \(x\in[-6;\,2]\). Отметив точки в координатной плоскости, координаты которых указаны в таблице, и соединив их плавной непрерывной линией, получим график искомой функции \(y=-0{,}25x^{2}\) на заданном промежутке.

Функция \(y=-0,25x^{2}\) — парабола, ветви которой направлены вниз, так как \(a = -0,25 < 0\), поэтому её наибольшее значение находится в вершине.

У функции вида \(y=ax^{2}\) вершина всегда в точке \((0,0)\). Значит, \( y_{\text{наиб.}}=0\) при \( x=0\).

Наименьшее значение на ограниченном промежутке достигается либо в вершине, либо на концах. Значения на концах равны \(-9\) и \(-1\). Значит, \( y_{\text{наим.}}=-9\) при \( x=-6\).