Упражнение 193 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 69

а) \(y=ax^{2}\)

Если \(a>0\), то ветви параболы направлены вверх и \(E(f) =[0;\,+\infty)\)

б) \(y=ax^{2}\)

Если \(a < 0\), то ветви параболы направлены вниз и \(E(f) =(-\infty;\,0]\)

Пояснения:

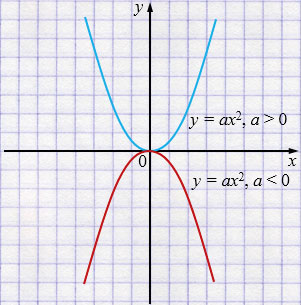
Функция \(y=ax^{2}\) — парабола с вершиной в начале координат.

Если \(a>0\), то ветви параболы направлены вверх, поэтому \( y \ge 0\), что соответствует промежутку значений \([0;+\infty).\)

Если \(a<0\), то ветви параболы направлены вниз, поэтому \( y \le 0\), что соответствует промежутку \((-\infty;0].\)