Упражнение 270 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 91

а) \(3x^2 + bx + 3 = 0\)

\(D = b^2 - 4\cdot 3 \cdot 3 = b^2 - 36\)

\(b^2 - 36 > 0\)

\(y = b^2 - 36\) - парабола, ветви которой направлены вверх.

\(b^2 - 36 = 0\)

\(b^2 = 36\)

\(b = \pm \sqrt {36}\)

\(b = \pm6\)

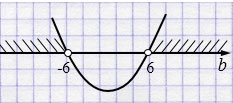
Ответ: \(b \in (-\infty; -6) \cup (6; +\infty)\).

б) \(x^2 + 2bx + 15 = 0\)

\(D = (2b)^2 - 4\cdot 1 \cdot 15 =\)

\(=4b^2 - 60.\)

\(4b^2 - 60 > 0\)

\(y = 4b^2 - 60\) - парабола, ветви которой направлены вниз.

\(4b^2 - 60 = 0\)

\(4b^2 = 60\)

\(b^2 = \frac{60}{4}\)

\(b^2 = 15\)

\(b = \pm \sqrt{15}\)

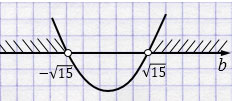
Ответ: \(b \in (-\infty; -\sqrt{15}) \cup (\sqrt{15}; +\infty)\).

Пояснения:

Основное правило:

Квадратное уравнение \(ax^2 + bx + c = 0\) имеет два различных корня, если дискриминант:

\[D = b^2 - 4ac > 0.\]

Решение неравенств вида

\(ax^2 + с > 0\):

1) находим корни уравнения

\(ax^2 + c = 0\).

2) отмечаем корни уравнений на оси \(x\) и через отмеченные точки проводим схематически параболу, ветви которой направлены вверх при \(a > 0\) или вниз при \(a < 0\);

3) находят на оси \(x\) промежутки, для которых точки параболы расположены выше оси \(x\).

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.

Чтобы найти корни уравнения \(ax^2 + c = 0\), переносим коэффициент \(c\) в правую сторону: \(ax^2  = -с\), затем делим обе части уравнения на \(a\): \(x^2  = \frac{-с}{a}\), откуда получаем

\(x_1 = -\sqrt{\frac{-c}{a}}\) и \(x_2= \sqrt{\frac{-c}{a}}\).