Упражнение 275 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 91
Вернуться к содержанию учебника
Вопрос
(Для работы в парах.) Докажите, что при любом значении переменной верно неравенство:
а) \(7x^{2}-10x+7>0\);
б) \(-6y^{2}+11y-10<0\);
в) \(4x^{2}+12x+9\ge0\);
г) \(\dfrac14x^{2}-8x+64\ge0\);
д) \(-9y^{2}+6y-1\le0\);
е) \(-5x^{2}+8x-5<0\).
1) Обсудите, при каком условии неравенство \(ax^{2}+bx+c>0\), где \(a,b,c\) — некоторые числа, верно при любом значении переменной \(x\). Укажите аналогичные условия для неравенства \(ax^{2}+bx+c<0\).
2) Распределите, кто выполняет задания а), в), д), а кто — задания б), г), е), и выполните их.
3) Проверьте друг у друга, правильно ли выполнено доказательство неравенств, и исправьте ошибки, если они допущены.
Подсказка
Вспомните:
- Решение неравенств второй степени с одной переменной.
- Квадратный трехчлен, его корни.
- Степень с натуральным показателем.
- Свойства степени с натуральным показателем.
- Квадратичную функцию, ее график.
- Деление и дроби.
- Деление рациональных чисел.
- Умножение рациональных чисел.
- Вычитание рациональных чисел.
- Десятичная запись дробных чисел.
- Сравнение рациональных чисел.
- Квадрат суммы и квадрат разности двух выражений.
- Линейное уравнение с одной переменной.
Ответ
1) \(ax^{2}+bx+c\)
\(D=b^{2}-4ac\).
\(ax^{2}+bx+c>0\) при всех \(x\), если одновременно \(a>0\) и \(D<0\).
\(ax^{2}+bx+c<0\) при всех \(x\), если одновременно \(a<0\) и \(D<0\).
2) а) \(7x^{2}-10x+7>0\)
\(y = 7x^{2}-10x+7\) - парабола, ветви которой направлены вверх, так как \(a = 7> 0\).
\(7x^{2}-10x+7 = 0\)
\(D=(-10)^{2}-4\cdot7\cdot7=\)
\(=100-196=-96<0\) - корней нет.
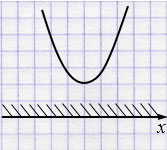
\(7x^{2}-10x+7>0\) при любом \(x\).
б) \(-6y^{2}+11y-10<0\)
\(x = -6y^{2}+11y-10\) - парабола, ветви которой направлены вниз, так как \(a = -6 < 0\).
\(-6y^{2}+11y-10 = 0\)
\(D=11^{2}-4\cdot(-6)\cdot(-10)=\)
\(=121-240=-119<0\) - корней нет.
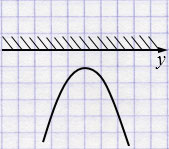
\(-6y^{2}+11y-10<0\) при любом \(y\).
в) \(4x^{2}+12x+9\ge0\)
\(y = 4x^{2}+12x+9\) - парабола, ветви которой направлены вверх, так как \(a = 4 > 0\).
\(4x^{2}+12x+9=0\)
\((2x)^{2}+2\cdot2x\cdot3+3^{2}=0\)
\((2x + 3)^2 = 0\)
\(2x+3=0\)
\(2x = -3\)
\(x = -\frac32\)
\(x = -1,5\)

\(4x^{2}+12x+9\ge0\) при любом \(x\)
г) \(\dfrac14x^{2}-8x+64\ge0\)
\(y = \dfrac14x^{2}-8x+64\) - парабола, ветви которой направлены вверх, так как \(a = \frac14 > 0\).
\(\dfrac14x^{2}-8x+64 = 0\) \(/\times 4\)
\(x^2 - 32x + 256 = 0\)
\((x-16)^{2} = 0\)
\(x - 16 = 0\)
\(x = 16\)
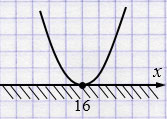
\(\dfrac14x^{2}-8x+64\ge0\) при любом \(x\).
д) \(-9y^{2}+6y-1\le0\)
\(x = -9y^{2}+6y-1\) - парабола, ветви которой направлены вниз, так как \(a = -9 < 0\).
\(-9y^{2}+6y-1=0\) \(/\times (-1)\)
\(9y^{2}-6y+1=0\)
\((3y-1)^{2} = 0\)
\(3y = 1\)
\(y = \frac13\)
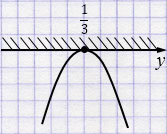
\(-9y^{2}+6y-1\le0\) при любом \(y\)
е) \(-5x^{2}+8x-5<0\)
\(y =-5x^{2}+8x-5\) - парабола, ветви которой направлены вниз.
\(-5x^{2}+8x-5=0\) \(/\times (-1)\)
\(5x^{2}-8x+5=0\)
\(D=(-8)^{2}-4\cdot5\cdot5=\)
\(=64-100=-36<0\) - корней нет.
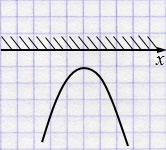
\(-5x^{2}+8x-5<0\) при любом \(x\).
Пояснения:
Общие правила для квадратных неравенств.
Квадратный трёхчлен \(ax^{2}+bx+c\) имеет дискриминант
\[D=b^{2}-4ac.\]
Если \(D<0\), то у уравнения
\(ax^{2}+bx+c=0\) нет действительных корней, а парабола не пересекает ось \(Ox\).
Тогда знак трёхчлена совпадает со знаком коэффициента \(a\) при любых \(x\):
• если \(a>0\) и \(D<0\), то
\(ax^{2}+bx+c>0\) для всех \(x\);
• если \(a<0\) и \(D<0\), то
\(ax^{2}+bx+c<0\) для всех \(x\).
Если \(D=0\), то трёхчлен можно записать как полный квадрат, учитывая формулы квадрата суммы и квадрата разности:
\((a + b)^2 = a^2 + 2ab + b^2\),
\((a - b)^2 = a^2 - 2ab + b^2\).
и знак определяется знаком \(a\): при \(a>0\) получаем \(\ge0\), при \(a<0\) получаем \(\le0\); нуль достигается в одной точке.
Вернуться к содержанию учебника