Упражнение 279 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 92

Пусть ширина прямоугольника равна \(x\) (\(x > 0\)), тогда длина равна \(x + 5\).

Площадь прямоугольника:

\( x(x + 5)\).

Составим неравенство:

\(x(x + 5) > 36\).

\(x^2 + 5x > 36\)

\(x^2 + 5x - 36 > 0\)

\(y = x^2 + 5x - 36\) - парабола, ветви которой направлены вверх.

\(x^2 + 5x - 36 = 0\)

\(D = 5^2 - 4\cdot 1 \cdot (-36) = \)

\(=25 + 144 = 169 > 0\) - 2 корня.

\(\sqrt{169} = 13\)

\(x_1 = \frac{-5 - 13}{2} = \frac{-18}{2} = -9\)

\(x_2 = \frac{-5 + 13}{2} = \frac{8}{2} = 4\)

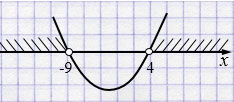
\(x \in (-\infty; -9) \cup (4; +\infty)\)

По условию (\(x > 0\), поэтому

\(x \in (4; +\infty)\)

Ответ: ширина прямоугольника должна быть больше 4 см.

Пояснения:

Основные правила.

1. Если площадь \(x(x+5) > 36\), то получаем квадратное неравенство.

2. Для квадратного трёхчлена

\(ax^2+bx+c\) вычисляют дискриминант:

\(D=b^2-4ac\), который получается больше нуля и находят корни:

\(x_{1,2} = \frac{-b \pm \sqrt D}{2a}\)

3. отмечаем корни на оси \(x\) и через отмеченные точки проводим схематически параболу, ветви которой направлены вверх при \(a > 0\).

4. находят на оси \(x\) промежутки, для которых точки параболы расположены выше оси \(x\).

5. так как речь идёт о длине, значение должно быть положительным, поэтому из полученных промежутков берем только положительные значения.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.