Упражнение 305 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 103

1) \( y = x^{4} - ax^{3} - 10x^{2} + 80x - 96 \)

\((4;\,0)\)

\( 4^{4} - a\cdot4^{3} - 10\cdot4^{2} + 80\cdot4 - 96 = 0\)

\( 256 - 64a - 160 + 320 - 96 = 0\)

\( 320 - 64a = 0\)

\( 64a = 320\)

\(a = \frac{320}{64}\)

\(a = 5\)

2) \( y = x^{4} - 5x^{3} - 10x^{2} + 80x - 96\)

С осью \(x\):  \(y = 0\).

\(x = 4\) — корень уравнения.

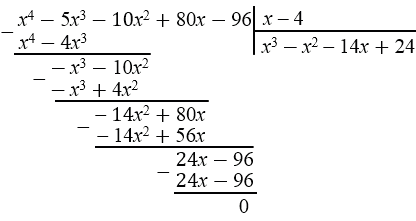
\( x^{4} - 5x^{3} - 10x^{2} + 80x - 96 = (x - 4)(x^{3} - x^{2} - 14x + 24)\)

\( (x - 4)(x^{3} - x^{2} - 14x + 24)=0\)

\((x^{3} - x^{2} - 14x + 24)=0\)

\(\pm1,\pm2,\pm3,\pm4,\pm6,\pm8,\pm12,\pm24\) - делители числа 24.

Если \(x = 2\), то

\( 2^{3} - 2^{2} - 14\cdot2 + 24 =0\)

\(8 - 4 - 28 + 24 = 0\)

\(0 = 0\)  - верно.

\(x = 2\) — корень уравнения.

\((2; 0)\) - точка пересечения с осью \(x\).

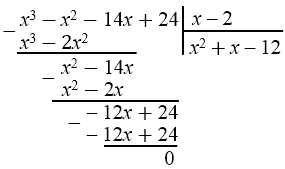
\( x^{3} - x^{2} - 14x + 24 = (x - 2)(x^{2} + x - 12)\)

\((x - 2)(x^{2} + x - 12)=0\)

\(x^{2} + x - 12 = 0\)

\(D = 1^2 - 4\cdot1\cdot(-12) =\)

\(=1 + 48 = 49 > 0\) - 2 корня.

\(\sqrt{49} = 7\).

\(x_1 = \frac{-1 + 7}{2\cdot1} = \frac{6}{2} = 3\).

\(x_2 = \frac{-1 - 7}{2\cdot1} = \frac{-8}{2} = -4\).

\((3; 0),\, (-4; 0)\) - точки пересечения с осью \(x\).

Ответ: \(a = 5\), \((2,0),\, (-4,0),\, (3,0). \)

Пояснения:

Если точка \((x_0,0)\) лежит на графике, то \(x_0\) — корень уравнения, значит подстановка даёт уравнение для нахождения \(a\).

Чтобы найти точки пересечения с \(Ox\), нужно решить уравнение \(y = 0\).

По условию \((4; 0)\) точка на графике рассматриваемой функции, значит, \(x = 4\) - корень уравнения. Используя этот корень, раскладываем многочлен на множители, для этого делим многочлен \(x^{4} - ax^{3} - 10x^{2} + 80x - 96\) на \((x - 4)\) (столбиком) и получаем многочлен меньшей степени (третьей). Процесс можно повторять, пока степень не станет 2, при этом учитываем то, что если многочлен имеет целый корень, то он является делителем свободного члена (последнего числового коэффициента). В данном случае, мы определили, что корнем многочлена \( x^{3} - x^{2} - 14x + 24\) является число \(2\). Снова разделили уголком многочлен на \((x - 2)\) и получили многочлен второй степени.

Квадратное уравнение

\(ax^{2} + bx + c = 0\)

решается через дискриминант

\(D = b^2 - 4ac\).

Если \(D > 0\), то уравнение имеет 2 корня:

\[ x_{1,2} = \dfrac{-b \pm \sqrt{D}}{2a}. \]