Упражнение 911 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 205
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№911 учебника 2023-2025 (стр. 205):
Изобразите на координатной прямой промежуток и назовите его:
а) \([-2; 4]\);
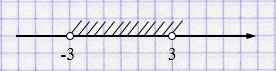
б) \((-3; 3)\);
в) \([0; 5]\);
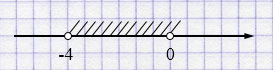
г) \((-4; 0)\);
д) \((3; +\infty)\);
е) \([2; +\infty)\);
ж) \((-\infty; 4]\);
з) \((-\infty; -1)\);
и) \((-\infty; +\infty)\).
№911 учебника 2013-2022 (стр. 205):
Докажите, что при \(a>0,\; b>0,\; c>0\) верно неравенство \[ \frac{3}{a+b+c}<\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}. \]
Подсказка
№911 учебника 2023-2025 (стр. 205):
Вспомните виды числовых промежутков.
№911 учебника 2013-2022 (стр. 205):
Вспомните:
- Доказательство неравенств.
- Рациональные дроби.
- Сложение рациональных дробей с одинаковыми знаменателями.
- Сравнение дробей.
Ответ
№911 учебника 2023-2025 (стр. 205):
а) \([-2; 4]\) — числовой отрезок.

б) \((-3; 3)\) — интервал.
в) \([0; 5]\) — числовой отрезок.

г) \((-4; 0)\) — интервал.
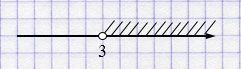
д) \((3; +\infty)\) — открытый числовой луч.
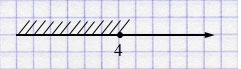
е) \([2; +\infty)\) — числовой луч.

ж) \((-\infty; 4]\) — числовой луч.
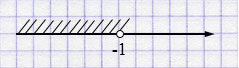
з) \((-\infty; -1)\) —открытый числовой луч.
и) \((-\infty; +\infty)\) — вся числовая прямая.

№911 учебника 2013-2022 (стр. 205):
\(\frac{3}{a+b+c}<\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\)
\(a>0,\; b>0,\; c>0\).
\( \frac{1}{a+b+c}+\frac{1}{a+b+c} +\frac{1}{a+b+c} < \frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\)
\(\frac{1}{a+b+c} < \frac{1}{a+b}\),
\(\frac{1}{a+b+c} < \frac{1}{b+c}\),
\(\frac{1}{a+b+c} < \frac{1}{c+a}\)
Следовательно,
\(\frac{3}{a+b+c}<\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\)
при \(a>0,\; b>0,\; c>0\).
Что и требовалось доказать.
Пояснения:
При доказательстве помним, чем меньше слагаемые в сумме, тем меньше будет сумма, и то, что из двух дробей с одинаковыми числителями меньше та дробь, у которой знаменатель больше.
Вернуться к содержанию учебника