Упражнение 915 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

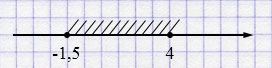
а) \(-1,5 \leq x \leq 4\)

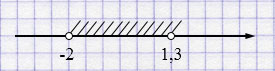
б) \(-2 < x < 1,3\)

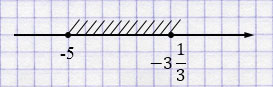
в) \(-5 \leq x \leq -3 \frac{1}{3}\)

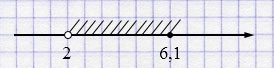
г) \(2 < x \leq 6,1\)

Пояснения:

Двойное неравенство ограничивает \(x\) с двух сторон.

Правила:

Если в неравенстве используется \(\leq\) или \(\geq\), то соответствующая граница включается и отмечается закрашенной точкой.

Если используется строгий знак \(<\) или \(>\), то граница не включается и отмечается пустым кружком.

а) \((6y-1)(y+2) < (3y+4)(2y+1)\)

\((6y-1)(y+2) - (3y+4)(2y+1) =\)

\(=6y^2 + 12y - y - 2 - (6y^2 + 3y + 8y + 4) =\)

\(=\cancel{6y^2} + \cancel{12y} - \cancel y - 2 - \cancel{6y^2} - \cancel{3y} - \cancel{8y} - 4 =\)

\(=-2 < 0\).

Неравенство доказано.

б) \((3y-1)(2y+1) > (2y-1)(2+3y)\)

\((3y-1)(2y+1) - (2y-1)(2+3y)=\)

\(=6y^2 + 3y -2y - 1 - (4y +6y^2 -2 -3y)=\)

\(=\cancel{6y^2} + \cancel{3y} - \cancel{2y} - 1 - \cancel{4y} - \cancel{6y^2} + 2 + \cancel{3y})=\)

\(= 1 > 0\)

Неравенство доказано.

Пояснения:

При доказательстве находим разность левой и правой частей неравенства и учитываем то, что:

- если \(a - b < 0\), то \(a < b\),

- если \(a - b > 0\), то \(a > b\).