Упражнение 910 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

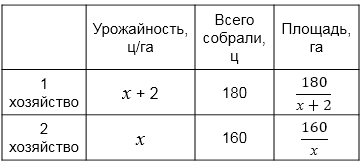
Составим уравнение:

\(\frac{160}{x} - \frac{180}{x+2} = 1\)  \(/\times x(x+2)\)

ОДЗ: \(x \neq 0\)   и   \(x + 2 \neq 0\)

                           \(x \neq -2\)

\(160(x+2) - 180x = x(x+2)\)

\(160x + 320 - 180x = x^2 + 2x\)

\(-20x + 320 = x^2 + 2x\)

\(x^2 + 2x + 20x - 320 = 0\)

\(x^2 + 22x - 320 = 0\)

\(a = 1\),  \(b = 22\),  \(c = - 320\)

\( D = b^2 - 4ac =\)

\(=22^2 - 4 \cdot 1 \cdot (-320) = \)

\(=484 + 1280 = 1764\),    \( \sqrt{D} = 42\).

\( x_1 = \frac{-22 + 42}{2\cdot1} = \frac{20}{2} = 10\)

\( x_2 = \frac{-22 - 42}{2\cdot1} = \frac{-64}{2} = -32\) - не удовлетворяет условию.

1) \(10\) (ц/га) - урожайность во втором хозяйстве.

2) \(10+ 2 = 12\) ( ц/га) - урожайность в первом хозяйстве.

Ответ: урожайность гречихи в первом хозяйстве — 12 ц/га, а во втором — 10 ц/га.

Пояснения:

Обозначили за \(x\) ц/га урожайность во втором хозяйстве, тогда урожайность в первом хозяйстве \(x + 2\) ц/га. В первом хозяйстве собрали 180 ц гречихи, а во втором —  только 160 ц. Чтобы найти площадь, нужно весь собранный урожай с этой площади разделить на урожайность. Значит, площадь под гречихой в первом хозяйстве \( \frac{180}{x+2}\) га, а площадь под гречихой во втором хозяйстве \(\frac{160}{x}\) га. Известно, что во втором хозяйстве под гречиху было отведено на 1 га больше, чем в первом хозяйстве, следовательно, можем составить дробное рациональное уравнение:

\(\frac{160}{x} - \frac{180}{x+2} = 1\).

Алгоритм решения дробного рационального уравнения:

1) найти ОДЗ (область допустимых значений), то есть те значения переменной, при которых знаменатель обращается в нуль;

2) найти общий знаменатель дробей, входящих в уравнение;

3) умножить обе части уравнения на общий знаменатель;

4) решить получившееся целое уравнение;

5) исключить из его корней те, которые совпадают с ОДЗ.

В ходе преобразований получили полное квадратное уравнение, у которого дискриминант \(D\) больше нуля, поэтому уравнение имеет два корня:

\(x_1 =\frac{-b+\sqrt{D}}{2a}\);

\(x_2 =\frac{-b-\sqrt{D}}{2a}\).

Мы получили два значения \(10\) и \(-32\). Но отрицательное значение не подходит, так как урожайность не может быть отрицательным числом. Следовательно, урожайность во втором хозяйстве равна \(10\) ц/га. Урожайность в первом хозяйстве на \(2\) ц/га больше, значит, урожайность в первом хозяйстве \(12\) ц/га.

\[ \sqrt{(a+c)(b+d)} \ge \sqrt{ab}+\sqrt{cd}, \] если \(a>0,\; b>0,\; c>0,\; d>0\).

\[ (a+c)(b+d) \;\ge\; \bigl(\sqrt{ab}+\sqrt{cd}\bigr)^2 \]

\[ ab+ad+bc+cd \;\ge\; (\sqrt{ab})^2 + 2\sqrt{ab}\cdot\sqrt{cd} + (\sqrt{cd})^2 \]

\[ ab+ad+bc+cd \;\ge\; ab + 2\sqrt{abcd} + cd \]

\[ \cancel{ab}+ad+bc+\cancel{cd}-\cancel{ab}-\cancel{cd} \;\ge\; 2\sqrt{abcd}. \]

\[ ad+bc \;\ge\; 2\sqrt{abcd}. \]

\[ ad-2\sqrt{abcd}+bc \;\ge\; 0 \]

\[ (\sqrt{ad})^2-2\sqrt{abcd}+(\sqrt{bc})^2 \;\ge\; 0 \]

\( (\sqrt{ad}-\sqrt{bc})^2 \;\ge\; 0 \) - верно при любых \(a>0,\; b>0,\; c>0,\; d>0\).

Пояснения:

При доказательстве используем то, что если левая и правая части верного неравенства положительные числа, то при возведении их в квадрат получится верное неравенство.

Квадрат суммы двух выражений:

\((a + b)^2 = a^2 + 2ab + b^2\).

Квадрат разности двух выражений:

\((a - b)^2 = a^2 - 2ab + b^2\).

Свойства корня:

\((\sqrt a)^2 = a)\);

\(\sqrt a \cdot \sqrt b = \sqrt {ab}\).