Упражнение 914 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

а) \(x \geq -2\)

б) \(x \leq 3\)

в) \(x > 8\)

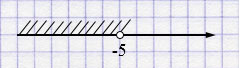
г) \(x < -5\)

д) \(x > 0{,}3\)

е) \(x \leq -8{,}1\)

Пояснения:

а) \(x \geq -2\). Значит, точка -2 закрашена, и решение идёт вправо: \([-2; +\infty)\).

б) \(x \leq 3\). Значит, точка 3 закрашена, и решение идёт влево: \((-\infty; 3]\).

в) \(x > 8\). Точка 8 пустая, решение идёт вправо: \((8; +\infty)\).

г) \(x < -5\). Точка -5 пустая, решение идёт влево: \((-\infty; -5)\).

д) \(x > 0{,}3\). Точка 0,3 пустая, решение идёт вправо: \((0,3; +\infty)\).

е) \(x \leq -8{,}1\). Точка -8,1 закрашена, решение идёт влево: \((-\infty; -8,1]\).

Пусть расстояние в одну сторону равно \(s\) км, а намеченная скорость равна

\(x\) км/ч (\(x>2\)).

1) Время по плану:

\(\dfrac{s}{x} + \dfrac{1}{2}+\dfrac{s}{x}= \dfrac{2s}{x}+\dfrac{1}{2}\) (ч)

2) Время по факту:

\(\dfrac{s}{\,x-2\,}+\dfrac{1}{2}+\dfrac{s}{\,x+2\,}\) (ч)

3) \(\dfrac{2s}{x}+\dfrac{1}{2} \; {\color{red}{?}} \; \dfrac{s}{\,x-2\,}+\dfrac{1}{2}+\dfrac{s}{\,x+2\,}\)

\(\dfrac{2s}{x} \; {\color{red}{?}} \; \dfrac{s}{\,x-2\,} +\dfrac{s}{\,x+2\,} \)  \(/ : s\)

\(\dfrac{2}{x} \; {\color{red}{?}} \; \dfrac{1}{\,x-2\,} ^{\color{blue}{\backslash x+2}} +\dfrac{1}{\,x+2\,} ^{\color{blue}{\backslash x-2}} \)

\(\dfrac{2}{x} \; {\color{red}{?}} \; \dfrac{(x+2)+(x-2)}{\,(x-2)(x+2)\,}\)

\(\dfrac{2}{x} \; {\color{red}{?}} \; \dfrac{x+2+x-2}{\,x^2-4\,}\)

\(\dfrac{2}{x} \; {\color{red}{?}} \; \dfrac{2x}{\,x^2-4\,}\)

\(\dfrac{2x}{x^2} \; {\color{red}{?}} \; \dfrac{2x}{\,x^2-4\,}\)

\(x^2 > x^2 - 4\)

\(\dfrac{2x}{x^2} \; {\color{red}{<}} \; \dfrac{2x}{\,x^2-4\,}\)

Ответ: велосипедист не успел вернуться в посёлок к назначенному сроку.

Пояснения:

Чтобы найти время, нужно расстояние разделить на скорость.

Расстояние между поселком и городом обозначаем \(s\) км, а плановую скорость \(x\) км/ч.

Плановое время — сумма времён «туда» и «обратно» при скорости \(x\) плюс \(\frac12\) часа в городе.

Фактическое время — то же время в городе \(\frac12\) ч, время туда и обратно при скоростях \(x-2\) и \(x+2\) соответственно.

Чтобы ответить на вопрос, успел ли велосипедист вернуться в посёлок к назначенному сроку, нужно сравнить плановое время и фактическое время.

При сравнении выражение, соответствующее фактическому времени, приводим к общему знаменателю. А в выражении, соответствующем плановому времени, домножаем числитель и знаменатель на \(x\). Получили:

\(\dfrac{2x}{x^2} \; {\color{red}{?}} \; \dfrac{2x}{\,x^2-4\,}\).

Чем больше знаменатель дроби, тем меньше дробь.

\(x^2 > x^2 - 4\), поэтому

\(\dfrac{2x}{x^2} \; {\color{red}{<}} \; \dfrac{2x}{\,x^2-4\,}\).

Значит, велосипедист не успел вернуться в посёлок к назначенному сроку.