Упражнение 1156 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 258
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№1156 учебника 2023-2025 (стр. 258):
Какой из трёх графиков, изображённых на рисунке 77, является графиком функции \(y = |x - 2|\)?
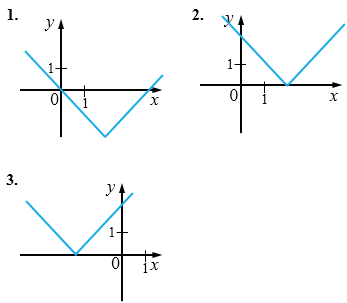
Рис. 77
Подсказка
№1156 учебника 2023-2025 (стр. 258):
Вспомните:
- Что называют функцией, ее область определения и область значений.
- График функции.
- Модуль числа.
- Числовые промежутки.
- Линейное уравнение с одной переменной.
- Координаты точки.
Ответ
№1156 учебника 2023-2025 (стр. 258):
\(y = |x - 2|\)
\(D(y) = (-\infty; +\infty)\)
\(E(y) = [0; +\infty)\)
\( |x - 2| = 0\)
\( x - 2 = 0\)
\(x = 2\)
\((2; 0)\) - точка пересечения с осью \(x\)
Ответ: график функции \(y = |x - 2|\) изображён под номером 2.
Пояснения:
Область определения функции
\(y = |x - 2|\):
\(D(y) = (-\infty; +\infty)\), так как значения \(x\) могут быть любыми.
Область значений функции
\(y = |x - 2|\):
\(E(y) = [0; +\infty)\), так как модуль принимает только неотрицательные значения.
При пересечении графика с осью \(x\) значения функции равны нулю, то есть \(y = 0\).
Чтобы определить координаты точек пересечения графика функции
\(y = |x - 2|\) с осью \(x\), решаем уравнение:
\( |x - 2| = 0\), откуда \(x = 2\).
Значит, \((2; 0)\) - точка пересечения графика функции \(y = |x - 2|\) с осью \(x\). Следовательно, графиком функции \(y = |x - 2|\) является график под номером 2.
Вернуться к содержанию учебника