Упражнение 1164 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 259
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№1164 учебника 2023-2025 (стр. 259):
Постройте график функции и перечислите её свойства:
а) \( y=\begin{cases} x^2, если \; x\le 1,\\ \sqrt{x}, если\; x>1; \end{cases} \)
б) \( y=\begin{cases} (x-1)^2, если\; x\le 2,\\ -2x + 5, если \; 2 < x \le 3.\end{cases} \)
Подсказка
№1164 учебника 2023-2025 (стр. 259):
Вспомните:
- Что называют функцией, ее свойства.
- Квадратичная функция, ее график.
- Функция арифметического квадратного корня, ее график.
- Арифметический квадратный корень.
- Степень с натуральным показателем.
- Линейная функция, ее график.
- Числовые промежутки.
Ответ
№1164 учебника 2023-2025 (стр. 259):
а) \( y=\begin{cases} x^2, если \; x\le 1,\\ \sqrt{x}, если\; x>1 \end{cases} \)
1) \(y = x^2\) при \(x \le 1\)
| \(x\) | 1 | 0 | -1 | -2 | -3 |
| \(y\) | 1 | 0 | 1 | 4 | 9 |
2) \(y = \sqrt{x}\) при \(x>1\)
| \(x\) | 1 | 4 | 9 |
| \(y\) | 1 | 2 | 3 |
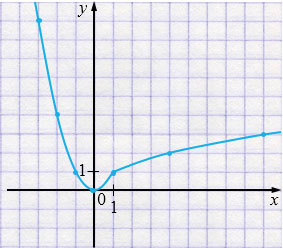
Свойства:
1. \(D(y) = (-\infty; +\infty)\).
2. \(E(y) = [0; +\infty)\).
3. Нули функции: \(y = 0\) при \(x = 0\).
4. \(y>0\) при \(x\in(-\infty; 0) \cup (0; +\infty)\).
5. Функция убывает при \(x\in(-\infty; 0] \),
функция возрастает при \(x\in[0; +\infty)\).
б) \( y=\begin{cases} (x-1)^2, если\; x\le 2,\\ -2x + 5, если \; 2 < x \le 3\end{cases} \)
1) \(y= (x-1)^2\) при \( x\le 2\)
| \(x\) | 2 | 1 | 0 | -1 | -2 |
| \(y\) | 1 | 0 | 1 | 4 | 9 |
2) \(y = -2x + 5\) при \(2 < x \le 3\)
| \(x\) | 2 | 3 |
| \(y\) | 1 | -1 |
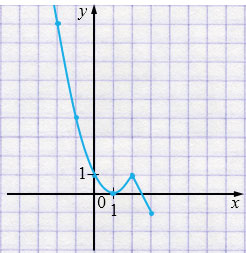
Свойства:
1. \(D(y) = (-\infty,3]\).
2. \(E(y) = [0; +\infty)\).
3. Нули функции: \(y = 0\) при
\(x = 0\) и \(x = 2,5\).
4. \(y>0\) при
\(x\in(-\infty; 1) \cup (1; 2,5)\).
\(y<0\) при \(x \in(2,5; 3]\).
5. Функция убывает при
\(x\in(-\infty; 1] \cup [2; 3] \),
функция возрастает при \(x\in[1;2]\).
Пояснения:
Правила построения кусочных функций: каждую часть строим на своём промежутке, по полученному графику описываем свойства функции:
1. Область определения функции \(D(f)\) - значения, которые может принимать переменная \(x\).
2. Область значений функции \(E(f)\) - значения, которые может принимать переменная \(y\).
3. Нули функции - значения аргумента, при которых функция обращается в нуль.
4. Промежутки знакопостоянства - промежутки, на которых функция сохраняет знак (на промежутках, расположенных выше оси \(x\) функция принимает положительные значения, на промежутках, расположенных ниже оси \(x\) функция принимает отрицательные значения).
3. Промежутки монотонности функции - промежутки возрастания и убывания функции.
Вернуться к содержанию учебника