Упражнение 1165 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 260
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№1165 учебника 2023-2025 (стр. 260):
С помощью графиков найдите приближённое значение корня уравнения \[ \sqrt{x} = \frac{2}{x}. \]
Подсказка
№1165 учебника 2023-2025 (стр. 260):
Ответ
№1165 учебника 2023-2025 (стр. 260):
\[ \sqrt{x} = \frac{2}{x} \]
1) \(y = \sqrt{x} \)
| \(x\) | 0 | 1 | 4 | 9 |
| \(y\) | 0 | 1 | 2 | 3 |
2) \(y = \frac{2}{x}\)
| \(x\) | 0,5 | 1 | 2 | 4 |
| \(y\) | 4 | 2 | 1 | 0,5 |
| \(x\) | -0,5 | -1 | -2 | -4 |
| \(y\) | -4 | -2 | -1 | -0,5 |
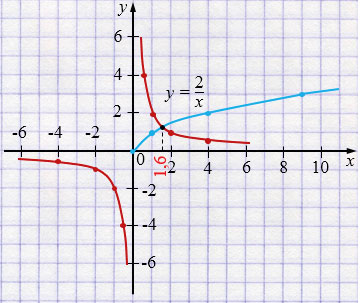
Ответ: \(x \approx 1{,}6.\)
Пояснения:
Чтобы с помощью графиков найти приближённое значение корня уравнения, нужно построить графики функций, стоящих в левой и правой частях уравнения и определить абсциссу (координату \(x)\) точек пересечения этих графиков.
Чтобы найти приближённое значение корня уравнения \( \sqrt{x} = \frac{2}{x} \), нужно построить графики функций \(y = \sqrt{x} \) и \(y = \frac{2}{x}\).
Функция \(y = \sqrt{x}\) определена при \(x\ge 0\), так как подкоренное выражение может принимать только неотрицательные значения.
Графиком функции \(y = \frac{2}{x}\) является гипербола, ветви которой расположены в 1 и 3 координатных четвертях, так как \(k = 2 > 0\).
Вернуться к содержанию учебника