Упражнение 1056 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1056 учебника 2023-2025 (стр. 232):
а) При каких \(x\) значение выражения \(2x - 4\) принадлежит интервалу \((-1; 5)\)?
б) При каких \(x\) значение дроби \(\dfrac{x - 5}{2}\) принадлежит числовому отрезку \([0; 5]\)?
в) При каких \(x\) значения функции \(y = -\dfrac{1}{3}x + 8\) принадлежат интервалу \((-1; 1)\)?
г) При каких \(x\) значения функции \(y = -2{,}5x + 6\) принадлежат числовому отрезку \([-6; -2]\)?
№1056 учебника 2013-2022 (стр. 240):
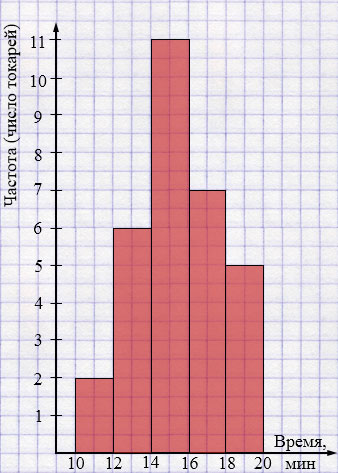
Наблюдая за работой бригады токарей, установили, сколько времени тратили они на обработку одной детали. Обобщая полученные данные, составили таблицу:
| Время, мин | Число токарей |
|
10–12 12–14 14–16 16–18 18–20 |
2 6 11 7 5 |
Пользуясь таблицей, постройте гистограмму, характеризующую распределение токарей бригады по времени, затрачиваемому на обработку одной детали.
Подсказка
№1056 учебника 2023-2025 (стр. 232):
Вспомните:
- Решение систем неравенств с одной переменной.
- Числовые промежутки.
- Решение неравенств с одной переменной.
- Деление и дроби.
- Деление рациональных чисел.
- Умножение рациональных чисел.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Деление десятичных дробей.
- Умножение обыкновенных дробей.
- Сокращение дробей.
№1056 учебника 2013-2022 (стр. 240):
Вспомните, что называют гистограммой.
Ответ
№1056 учебника 2023-2025 (стр. 232):
а) \(-1 < 2x - 4 < 5\)
\(\begin{cases} 2x-4 > -1, \\ 2x-4 < 5 \end{cases} \)
\(\begin{cases} 2x > -1 + 4, \\ 2x < 5 + 4 \end{cases} \)
\(\begin{cases} 2x > 3, / : 2\\ 2x < 9 / : 2 \end{cases} \)
\(\begin{cases} x > \frac32, \\ x < \frac92 \end{cases} \)
\(\begin{cases} x > 1,5, \\ x < 4,5 \end{cases} \)

Ответ: при \(x \in (1{,}5;\,4{,}5).\)
б) \(0 \le \dfrac{x - 5}{2} \le 5\)
\(\begin{cases} \dfrac{x - 5}{2} \ge 0, /\times2 \\ \dfrac{x - 5}{2} \le 10 /\times2 \end{cases} \)
\(\begin{cases} x - 5 \ge 0, \\ x - 5 \le 10 \end{cases} \)
\(\begin{cases} x \ge 5, \\ x \le 10 + 5 \end{cases} \)
\(\begin{cases} x \ge 5, \\ x \le 15 \end{cases} \)

Ответ: при \(x \in [5;\,15].\)
в) \(-1 < -\dfrac{1}{3}x + 8 < 1\)
\(\begin{cases} -\dfrac{1}{3}x + 8 > -1, /\times3 \\ -\dfrac{1}{3}x + 8 < 1 /\times3 \end{cases} \)
\(\begin{cases} -x + 24 > -3, /\times3 \\ -x + 24 < 3 /\times3 \end{cases} \)
\(\begin{cases} -x > -3 - 24, \\ -x < 3 - 24 \end{cases} \)
\(\begin{cases} -x > -27, /\times(-1) \\ -x < -21 /\times(-1) \end{cases} \)
\(\begin{cases} x < 27, \\ x > 21 \end{cases} \)

Ответ: при \(x \in (21;\,27).\)
г) \(-6 \le -2{,}5x + 6 \le -2\)
\(\begin{cases} -2{,}5x + 6 \ge -6, \\ -2{,}5x + 6 \le -2 \end{cases} \)
\(\begin{cases} -2{,}5x \ge -6 - 6, \\ -2{,}5x \le -2 - 6 \end{cases} \)
\(\begin{cases} -2{,}5x \ge -12, / : (-2,5) \\ -2{,}5x \le -8 / : (-2,5) \end{cases} \)
\(\begin{cases} x \le \frac{-12}{-2,5}, \\ x \ge \frac{-8}{-2,5} \end{cases} \)
\(\begin{cases} x \le \frac{120}{25}, \\ x \ge \frac{80}{25} \end{cases} \)
\(\begin{cases} x \le \frac{24}{5}, \\ x \ge \frac{16}{5} \end{cases} \)
\(\begin{cases} x \le 4,8, \\ x \ge 3,2 \end{cases} \)
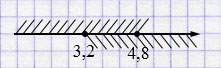
Ответ: при \(x \in [3{,}2;\,4{,}8].\)
Пояснения:
По условию составляем двойное неравенство. Двойное неравенство удобно раскладывать на систему из двух простых неравенств:
1) средняя часть больше левой части;
2) средняя часть меньше правой части.
Чтобы решить систему неравенств, нужно найти пересечение решений неравенств системы, то есть найти множество чисел, которое является одновременно решением и одного неравенства и решением другого неравенства. Если решения неравенств не пересекаются, то система решений не имеет.
При решении неравенств системы используем то, что:
- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;
- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство.
- если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.
Если знак неравенства строгий (\(>\) или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.
Если знак неравенства нестрогий (\(\geq\) или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.
№1056 учебника 2013-2022 (стр. 240):
Пояснения:
Гистограмма — это ступенчатая фигура, составленная из сомкнутых прямоугольников. Основание каждого прямоугольника равно длине интервала, а высота - частоте или относительной частоте. Таким образом, в гистограмме основания прямоугольников выбираются не произвольно, а строго определены длиной интервала.
По оси \(Ox\) откладываем интервалы времени в минутах:
\([10;12], [12;14], [14;16], [16;18], [18;20]\).
По оси \(Oy\) откладываем число токарей (частоту).
Строим прямоугольники:
— на промежутке \([10;12]\) высота прямоугольника равна \(2\);
— на промежутке \([12;14]\) высота равна \(6\);
— на промежутке \([14;16]\) высота равна \(11\);
— на промежутке \([16;18]\) высота равна \(7\);
— на промежутке \([18;20]\) высота равна \(5\).
По полученной гистограмме видно, что больше всего токарей тратят на обработку детали от \(14\) до \(16\) минут (столбец высотой \(11\)).
Меньше всего — от \(10\) до \(12\) минут (всего \(2\) токаря).
Вернуться к содержанию учебника