Упражнение 169 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№169 учебника 2023-2026 (стр. 66):
Постройте график функции:
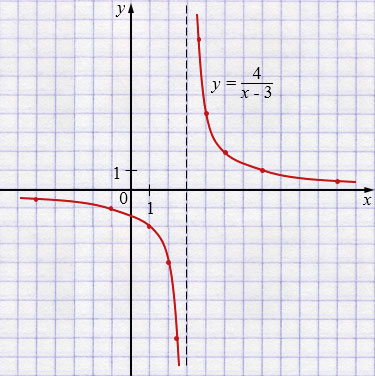
а) \(y=\dfrac{4}{x-3}\);
б) \(y=\dfrac{4}{x}+2\);
в) \(y=\dfrac{4}{x+3}\);
г) \(y=\dfrac{4}{x}-2\).
№169 учебника 2014-2022 (стр. 58):
Выразите корень \(n\)-й степени из отрицательного числа через арифметический корень той же степени:
а) \(\sqrt[3]{-31}\);
б) \(\sqrt[5]{-17}\);
в) \(\sqrt[11]{-2}\);
г) \(\sqrt[17]{-6}\).
Подсказка
№169 учебника 2023-2026 (стр. 66):
Вспомните:
- Дробно-линейную функцию, ее график.
- Координаты точки на координатной плоскости.
- Деление и дроби.
- Деление рациональных чисел.
- Десятичная запись дробных чисел.
№169 учебника 2014-2022 (стр. 58):
Вспомните:
- Корень \(n\)-й степени.
- Степень с натуральным показателем.
- Нечетные числа.
Ответ
№169 учебника 2023-2026 (стр. 66):
а) \(y=\dfrac{4}{x-3}\) - гипербола.
Вертикальная асимптота: \(x = 3\).
Горизонтальная асимптота: \(y = 0\).
| \(x\) | \(-5\) | \(-1\) | \(1\) | \(2\) | \(2,5\) |
| \(y\) | \(-0,5\) | \(-1\) | \(-2\) | \(-4\) | \(-8\) |
| \(x\) | \(3,5\) | \(4\) | \(5\) | \(7\) | \(11\) |
| \(y\) | \(8\) | \(4\) | \(2\) | \(1\) | \(0,5\) |
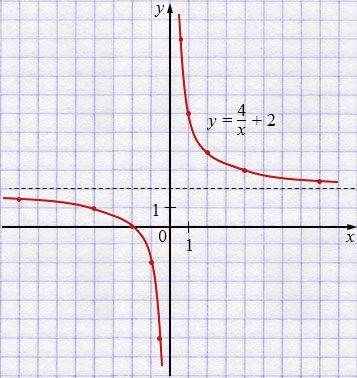
б) \(y=\dfrac{4}{x}+2\) - гипербола.
Вертикальная асимптота: \(x = 0\).
Горизонтальная асимптота: \(y = 2\).
| \(x\) | \(-8\) | \(-4\) | \(-2\) | \(-1\) | \(-0,5\) |
| \(y\) | \(1,5\) | \(1\) | \(0\) | \(-2\) | \(-6\) |
| \(x\) | \(0,5\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \(y\) | \(10\) | \(6\) | \(4\) | \(3\) | \(2,5\) |
в) \(y=\dfrac{4}{x+3}\)
Вертикальная асимптота: \(x = -3\).
Горизонтальная асимптота: \(y = 0\).
| \(x\) | \(-11\) | \(-7\) | \(-5\) | \(-4\) | \(-3,5\) |
| \(y\) | \(-0,5\) | \(-1\) | \(-2\) | \(-4\) | \(-8\) |
| \(x\) | \(-2,5\) | \(-2\) | \(-1\) | \(1\) | \(5\) |
| \(y\) | \(8\) | \(4\) | \(2\) | \(1\) | \(0,5\) |
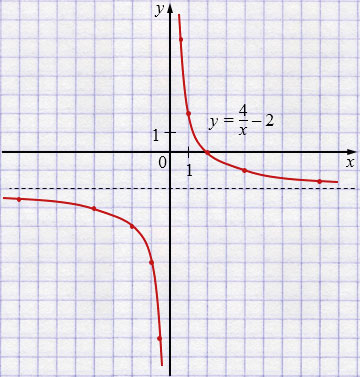
г) \(y=\dfrac{4}{x}-2\)
Вертикальная асимптота: \(x = 0\).
Горизонтальная асимптота: \(y = -2\).
| \(x\) | \(-8\) | \(-4\) | \(-2\) | \(-1\) | \(-0,5\) |
| \(y\) | \(-2,5\) | \(-3\) | \(-4\) | \(-6\) | \(-10\) |
| \(x\) | \(0,5\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \(y\) | \(6\) | \(2\) | \(0\) | \(-1\) | \(-1,5\) |
Пояснения:
Основные правила.
— График функции \(\displaystyle y=\frac{k}{x}\) — это гипербола, имеющая асимптоты:
\(x=0\) и \(y=0\).
Асимптота - это прямая, к которой график функции неограниченно приближается, но никогда не пересекает.
— Замена \(x\) на \((x-m)\) сдвигает график на \(m\) вправо.
— Замена \(x\) на \((x+m)\) сдвигает график на \(m\) влево.
— Добавление числа \(n\) сдвигает график вверх на \(n\) (если \(n>0\)) или вниз на \(|n|\) (если \(n<0\)).
Пояснение к пункту а).
\(y=\dfrac{4}{x-3}\) - графиком является гипербола, у которой вертикальная асимптота \(x=3\), горизонтальная асимптота \(y=0\). Поэтому график — гипербола \(y=\dfrac{4}{x}\), сдвинутая вправо на \(3\) единицы. Для построения графика функции пунктиром проводим асимптоту: прямую \(x = 3\). Так как гипербола состоит из двух ветвей, составляем две таблицы: одну для \(x < 3\), другую для \(x > 3\). Отметив точки в координатной плоскости, координаты которых указаны в первой таблице, и соединив их плавной непрерывной линией, получим одну ветвь гиперболы. Аналогично, используя вторую таблицу, получим вторую ветвь гиперболы.
Пояснение к пункту б).
\(y=\dfrac{4}{x}+2\) - графиком является гипербола, у которой вертикальная асимптота \(x=0\), горизонтальная асимптота \(y=2\). Поэтому график — гипербола \(y=\dfrac{4}{x}\), сдвинутая вверх на \(2\) единицы. Для построения графика функции пунктиром проводим асимптоту: прямую \(y = 2\). Так как гипербола состоит из двух ветвей, составляем две таблицы: одну для \(x < 0\), другую для \(x > 0\). Отметив точки в координатной плоскости, координаты которых указаны в первой таблице, и соединив их плавной непрерывной линией, получим одну ветвь гиперболы. Аналогично, используя вторую таблицу, получим вторую ветвь гиперболы.
Пояснение к пункту в).
\(y=\dfrac{4}{x+3}\) - графиком является гипербола, у которой вертикальная асимптота \(x=-3\), горизонтальная асимптота \(y=0\). Поэтому график — гипербола \(y=\dfrac{4}{x}\), сдвинутая влево на \(3\) единицы. Для построения графика функции пунктиром проводим асимптоту: прямую \(x = -3\). Так как гипербола состоит из двух ветвей, составляем две таблицы: одну для \(x < -3\), другую для \(x > -3\). Отметив точки в координатной плоскости, координаты которых указаны в первой таблице, и соединив их плавной непрерывной линией, получим одну ветвь гиперболы. Аналогично, используя вторую таблицу, получим вторую ветвь гиперболы.
Пояснение к пункту г).
\(y=\dfrac{4}{x}-2\) - графиком является гипербола, у которой вертикальная асимптота \(x=0\), горизонтальная асимптота \(y=-2\). Поэтому график — гипербола \(y=\dfrac{4}{x}\), сдвинутая вниз на \(2\) единицы. Для построения графика функции пунктиром проводим асимптоту: прямую \(y = 2\). Так как гипербола состоит из двух ветвей, составляем две таблицы: одну для \(x < 0\), другую для \(x > 0\). Отметив точки в координатной плоскости, координаты которых указаны в первой таблице, и соединив их плавной непрерывной линией, получим одну ветвь гиперболы. Аналогично, используя вторую таблицу, получим вторую ветвь гиперболы.
№169 учебника 2014-2022 (стр. 58):
а) \(\sqrt[3]{-31}=-\sqrt[3]{31}\)
б) \(\sqrt[5]{-17}=-\sqrt[5]{17}\)
в) \(\sqrt[11]{-2}=-\sqrt[11]{2}\)
г) \(\sqrt[17]{-6}=-\sqrt[17]{6}\)
Пояснения:
Здесь используется важное свойство корней нечётной степени:
\( \sqrt[n]{-a}=-\sqrt[n]{a}\), если \(n\) — нечётное.
Это свойство справедливо, потому что при нечётной степени знак числа сохраняется:
\[ (-b)^n=-b^n \]
А арифметический корень — это корень из положительного числа, который всегда неотрицательный.
Поэтому, чтобы выразить корень из отрицательного числа, нужно вынести знак «минус» перед корнем, а под корнем оставить положительное число.
Вернуться к содержанию учебника