Упражнение 620 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№620 учебника 2023-2025 (стр. 135):
Пусть  ,
,  ,
,  . Подставьте эти многочлены вместо
. Подставьте эти многочлены вместо  ,
,  и
и  в данное выражение и упростите его:
в данное выражение и упростите его:
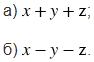
№620 учебника 2013-2022 (стр. 137):
Упростите выражение:
а) \(14y + 2y(6 - y);\)
б) \(3y^2 - 2y(5 + 2y);\)
в) \(4x(x - 1) - 2(2x^2 - 1);\)
г) \(5a(a^2 - 3a) - 3a(a^2 - 5a);\)
д) \(7b(4c - b) + 4c(c - 7b);\)
е) \(-2y(x^3 - 2y) - (x^3y + 4y^2);\)
ж) \(3m^2(m + 5n) - 2n(8m^2 - n);\)
з) \(6m^2n^3 - n^2(6m^2n + n - 1).\)
Подсказка
№620 учебника 2023-2025 (стр. 135):
Вспомните:
- Сложение и вычитание многочленов.
- Подобные слагаемые, раскрытие скобок.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
№620 учебника 2013-2022 (стр. 137):
Вспомните:
- Какое выражение называют одночленом.
- Какое выражение называют многочленом.
- Умножение одночлена на многочлен.
- Приведение подобных слагаемых.
- Свойства степени с натуральным показателем.
Ответ
№620 учебника 2023-2025 (стр. 135):
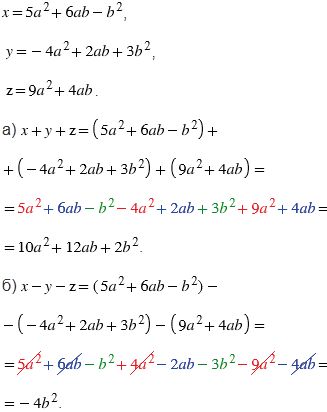
Пояснения:
Чтобы упростить выражения, сначала раскрываем скобки, учитывая знаки, стоящие перед ними (знак "минус" перед скобками меняет знаки слагаемых в скобках при раскрытии на противоположные), далее приводим подобные слагаемые (в решении выделены одинаковым цветом). Подобные слагаемые, которые в сумме дают ноль, вычеркнуты.
№620 учебника 2013-2022 (стр. 137):
а) \(14y + 2y(6 - y) = \)
\( = 14y + 12y - 2y^2 = 26y - 2y^2.\)
б) \(3y^2 - 2y(5 + 2y) = \)
\( =3y^2 - 10y - 4y^2 = -y^2 - 10y.\)
в) \(4x(x - 1) - 2(2x^2 - 1) = \)
\( = 4x^2 - 4x - 4x^2 + 2 = \)
\( = -4x + 2.\)
г) \(5a(a^2 - 3a) - 3a(a^2 - 5a) = \)
\( = 5a^3 - 15a^2 - 3a^3 + 15a^2 = 2a^3.\)
д) \(7b(4c - b) + 4c(c - 7b) = \)
\( = 28bc - 7b^2 + 4c^2 - 28bc = \)
\( = -7b^2 + 4c^2.\)
е) \(-2y(x^3 - 2y) - (x^3y + 4y^2) = \)
\( = -2x^3y + 4y^2 - x^3y - 4y^2 = \)
\( = -3x^3y.\)
ж) \(3m^2(m + 5n) - 2n(8m^2 - n) = \)
\( = 3m^3 + 15m^2n - 16m^2n + 2n^2 = \)
\( = 3m^3 - m^2n + 2n^2.\)
з) \(6m^2n^3 - n^2(6m^2n + n - 1) = \)
\( = 6m^2n^3 - 6m^2n^3 - n^3 + n^2 = \)
\( = -n^3 + n^2.\)
Пояснения:
Использованные правила и приёмы:
• Распределительный закон умножения: \(k(u + v) = ku + kv\), \(k(u - v) = ku - kv\).
• Приведение подобных членов: складываем коэффициенты при одинаковых переменных.
Комментарии к каждому пункту:
а) Умножили \(2y\) на каждый член в скобках, затем сложили с \(14y\).
б) Раскрыли скобки с минусом, получили \(3y^2 -10y -4y^2\), объединили \(y^2\)-члены.
в) Умножили \(4x\) и \(-2\) на соответствующие выражения и сократили \(4x^2\).
г) Раскрыли оба произведения \(a(\dots)\), сократили \(a^3\) и \(a^2\)-члены.
д) Умножили, заметив, что \(28bc\) сокращается при сложении.
е) Раскрыли скобки, затем \(4y^2\) и \(-4y^2\) взаимно уничтожились.
ж) Раскрыли оба произведения и объединили \(m^2n\)-члены: \(15 - 16 = -1\).
з) Раскрыли скобку с \(n^2\), получили противоположные члены \(6m^2n^3\).
Вернуться к содержанию учебника