Упражнение 615 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№615 учебника 2023-2025 (стр. 134):
Докажите, что при любом значении 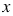 разность многочленов
разность многочленов  принимает положительное значение.
принимает положительное значение.
№615 учебника 2013-2022 (стр. 136):
Преобразуйте произведение в многочлен:
а) \(3ab(a^2 - 2ab + b^2)\);
б) \(-x^2y(x^2y^2 - x^2 - y^2)\);
в) \(2,5a^2b(4a^2 - 2ab + 0,2b^2)\);
г) \((-2ax^2 + 3ax - a^2)(-a^2x^2)\);
д) \((6,3x^3y - 3y^2 - 0,7x)\cdot 10x^2y^2\);
e) \(-1,4p^2q^6(5p^3q - 1,5pq^2 - 2q^3)\).
Подсказка
№615 учебника 2023-2025 (стр. 134):
Вспомните:
- Вычитание многочленов.
- Подобные слагаемые, раскрытие скобок.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Сложение и вычитание десятичных дробей.
- Степень с натуральным показателем.
- Сравнение рациональных чисел.
- Четные числа.
№615 учебника 2013-2022 (стр. 136):
Вспомните:
- Какое выражение называют одночленом.
- Какое выражение называют многочленом.
- Умножение одночлена на многочлен.
- Умножение рациональных чисел.
- Умножение десятичных дробей.
- Свойства степени с натуральным показателем.
Ответ
№615 учебника 2023-2025 (стр. 134):

Что и требовалось доказать.
Пояснения:
Составляем разность многочленов. Затем раскрываем скобки, учитывая знаки, стоящие перед ними (знак "минус" перед скобками меняет знаки слагаемых в скобках при раскрытии на противоположные), далее приводим подобные слагаемые (в решении выделены одинаковым цветом). Подобные слагаемые, которые в сумме дают ноль, вычеркнуты. И, учитывая, то что любое число в четной степени является неотрицательным числом, делаем вывод о том, что сумма неотрицательного числа и положительного числа при любом значении переменной будет положительным числом. Что и требовалось доказать.
№615 учебника 2013-2022 (стр. 136):
а) \(3ab(a^2 - 2ab + b^2) = \)
\( = 3ab\cdot a^2 - 3ab\cdot 2ab + 3ab\cdot b^2 =\)
\( =3a^3b - 6a^2b^2 + 3ab^3\).
б) \(-x^2y(x^2y^2 - x^2 - y^2) = \)
\( = -x^2y\cdot x^2y^2 + x^2y\cdot x^2 + x^2y\cdot y^2 = \)
\( =-x^4y^3 + x^4y + x^2y^3\).
в) \(2,5a^2b(4a^2 - 2ab + 0,2b^2) = \)
\( = 2{,}5a^2b\cdot4a^2 - 2{,}5a^2b\cdot2ab + 2{,}5a^2b\cdot0{,}2b^2 = \)
\( = 10a^4b - 5a^3b^2 + 0{,}5a^2b^3\).
г) \((-2ax^2 + 3ax - a^2)(-a^2x^2) = \)
\( = -2ax^2\cdot(-a^2x^2) + 3ax\cdot(-a^2x^2) - a^2\cdot(-a^2x^2) = \)
\(= 2a^3x^4 - 3a^3x^3 + a^4x^2\).
д) \((6,3x^3y - 3y^2 - 0,7x)\cdot10x^2y^2 = \)
\( = 63x^5y^3 - 30x^2y^4 - 7x^3y^2.\)
е) \(-1,4p^2q^6(5p^3q - 1,5pq^2 - 2q^3) = \)
\( = -1{,}4p^2q^6\cdot5p^3q + 1{,}4p^2q^6\cdot1{,}5pq^2 + 1{,}4p^2q^6\cdot2q^3 =\)
\(= -7p^5q^7 + 2{,}1p^3q^8 + 2{,}8p^2q^9\).
Пояснения:
Использованные правила:
Для каждого случая применён распределительный закон: множитель вне скобок умножается на каждый член внутри скобок.
\( X(Y+Z)=XY+XZ \).
Выполнены поочерёдно: возведение в степень, умножение коэффициентов и переменных с учётом показателей, затем приведены полученные одночлены.
Вернуться к содержанию учебника