Упражнение 1061 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1061 учебника 2023-2025 (стр. 208):
Принадлежит ли графику уравнения \(3x + 4y = 12\) точка:
а) \(A(4; 1)\);
б) \(B(1; 3)\);
в) \(C(-6; -7{,}5)\);
г) \(D(0; 3)\)?
№1061 учебника 2013-2022 (стр. 210):
Решите графически систему уравнений:
а) \( \begin{cases} x - 2y = 6, \\ 3x + 2y = -6; \end{cases}\)
б) \( \begin{cases} x - y = 0, \\ 2x + 3y = -5. \end{cases} \)
Подсказка
№1061 учебника 2023-2025 (стр. 208):
№1061 учебника 2013-2022 (стр. 210):
Ответ
№1061 учебника 2023-2025 (стр. 208):
а) \(x = 4\), \(y = 1:\)
\[ 3 \cdot 4 + 4 \cdot 1 = 12 + 4 = 16 \neq 12 \Rightarrow \text{не принадлежит} \]
б) \(x = 1\), \(y = 3:\)
\[ 3 \cdot 1 + 4 \cdot 3 = 3 + 12 = 15 \neq 12 \Rightarrow \text{не принадлежит} \]
в) \(x = -6\), \(y = -7{,}5:\)
\( 3 \cdot (-6) + 4 \cdot (-7{,}5) = -18 - 30 =\)
\(= -48 \neq 12 \Rightarrow \text{не принадлежит} \)
г) \(x = 0\), \(y = 3:\)
\[ 3 \cdot 0 + 4 \cdot 3 = 0 + 12 = 12 \Rightarrow \text{принадлежит} \]
Ответ: графику уравнения принадлежит только точка \(D(0; 3).\)
Пояснения:
Чтобы проверить принадлежность точки графику уравнения, нужно подставить координаты точки \(x\) и \(y\) в уравнение.
Если уравнение обращается в верное числовое равенство, то точка принадлежит графику. В противном случае — не принадлежит.
Из всех предложенных точек только точка \(D(0; 3)\) удовлетворяет уравнению \(3x + 4y = 12\).
№1061 учебника 2013-2022 (стр. 210):
а) \( \begin{cases} x - 2y = 6, \\ 3x + 2y = -6; \end{cases}\)
\(x - 2y = 6:\)
| \(x\) | 0 | 2 |
| \(y\) | -3 | -2 |
\(3x + 2y = -6:\)
| \(x\) | 0 | -2 |
| \(y\) | -3 | 0 |
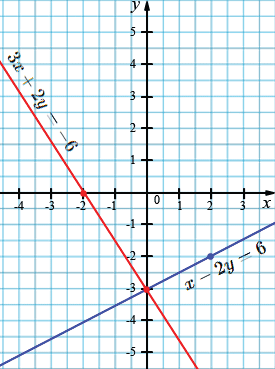
Ответ: \( (0; -3) \)
б) \( \begin{cases} x - y = 0, \\ 2x + 3y = -5. \end{cases} \)
\(x - y = 0:\)
| \(x\) | 0 | 3 |
| \(y\) | 0 | 3 |
\( 2x + 3y = -5:\)
| \(x\) | -1 | 2 |
| \(y\) | -1 | -3 |

Ответ: \( (-1; -1) \)
Пояснения:
Решение системы графически означает построение двух прямых на координатной плоскости и нахождение их точки пересечения (если она существует).
Вернуться к содержанию учебника