Упражнение 1065 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1065 учебника 2023-2025 (стр. 208):
Постройте график уравнения:
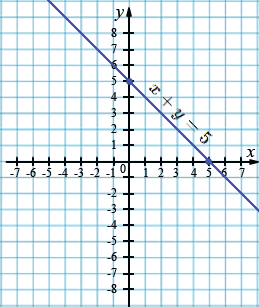
а) \(x+y=5;\)
б) \(y-4x=0;\)
в) \(1,6x=4,8;\)
г) \(0,5y=1,5.\)
№1065 учебника 2013-2022 (стр. 211):
Решите уравнение:
а) \(\dfrac{2x - 3}{4} - 3x = \dfrac{x + 1}{2}\)
б) \(6 = \dfrac{3x - 1}{3} - \dfrac{x}{5}\)
Подсказка
№1065 учебника 2023-2025 (стр. 208):
№1065 учебника 2013-2022 (стр. 211):
Ответ
№1065 учебника 2023-2025 (стр. 208):
а) \(x+y=5;\)
| \(x\) | 0 | 5 |
| \(y\) | 5 | 0 |
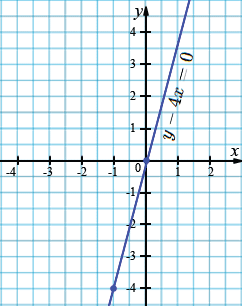
б) \(y-4x=0;\)
| \(x\) | 0 | -1 |
| \(y\) | 0 | -4 |
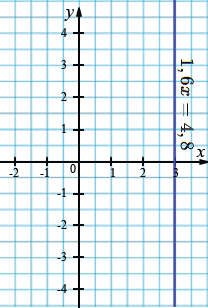
в) \(1,6x=4,8;\)
\(1,6x+0y=4,8;\)
\(x=\frac{4,8}{1,6};\)
\(x=3.\)
г) \(0,5y=1,5;\)
\(0,5y+0x=1,5;\)
\(y=\frac{1,5}{0,5};\)
\(y=3.\)

Пояснения:
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая. Прямая определяется двумя точками, поэтому чтобы построить график линейного уравнения с двумя переменными достаточно определить координаты каких-либо двух точек прямой.
№1065 учебника 2013-2022 (стр. 211):
а) \( \frac{2x - 3}{4} - 3x = \frac{x + 1}{2}; \) \(|\times4\)
\( 4 \cdot \left( \frac{2x - 3}{4} - 3x \right) = 4 \cdot \frac{x + 1}{2};\)
\( (2x - 3) - 12x = 2(x + 1); \)
\( 2x - 3 - 12x = 2x + 2;\)
\(-10x - 3 = 2x + 2;\)
\(-10x - 2x = 2+3;\)
\(-12x - 2x = 5;\)
\(-12x = 5;\)
\(x = -\frac{5}{12}. \)
Ответ: \(x = -\frac{5}{12}. \)
б) \( 6 = \frac{3x - 1}{3} - \frac{x}{5}; \) \(|\times15\)
\( 15 \cdot 6 = 15 \cdot \left( \frac{3x - 1}{3} - \frac{x}{5} \right);\)
\(90 = 5(3x - 1) - 3x;\)
\(90 = 15x - 5 - 3x;\)
\(90 = 12x - 5;\)
\(12x = 95;\)
\( x = \frac{95}{12}; \)
\( x =7 \frac{11}{12}. \)
Ответ: \( x =7 \frac{11}{12}. \)
Пояснения:
Метод домножения на общий знаменатель:
Чтобы исключить дроби в уравнении, можно умножить каждую часть уравнения на наименьший общий знаменатель (НОК) всех дробных выражений. Это избавляет от знаменателей и упрощает уравнение.
а) 1) НОК для 4 и 2 — это 4.
2) Домножение убрало знаменатели, уравнение стало линейным.
3) Решение: \( x = -\frac{5}{12} \).
б) 1) НОК для 3 и 5 — это 15.
2) Домножили обе части, избавились от дробей.
3) Решение: \( x =7 \frac{11}{12}. \)
Вернуться к содержанию учебника