Упражнение 1064 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1064 учебника 2023-2025 (стр. 208):
Постройте график уравнения:
а) \(2 𝑥 − 𝑦 = 6\);
б) \(1,5 𝑥 + 2 𝑦 = 3\);
в) \(𝑥 + 6 𝑦 = 0\);
г) \(0,5 𝑦 − 𝑥 = 1\);
д) \(1,2 𝑥 = − 4,8\);
е) \(1,5 𝑦 = 6\).
№1064 учебника 2013-2022 (стр. 211):
Укажите какие-нибудь три решения системы уравнений:
а) \( \begin{cases} x - 3y = 5, \\ 3x - 9y = 15; \end{cases}\)
б)\( \begin{cases} 1{,}5y + x = -0{,}5, \\ 2x + 3y = -1. \end{cases} \)
Подсказка
№1064 учебника 2023-2025 (стр. 208):
№1064 учебника 2013-2022 (стр. 211):
Ответ
№1064 учебника 2023-2025 (стр. 208):
а) \(2 𝑥 − 𝑦 = 6\);
| \(x\) | 0 | 3 |
| \(y\) | -6 | 0 |

б) \(1,5 𝑥 + 2 𝑦 = 3\);
| \(x\) | 0 | 2 |
| \(y\) | 1,5 | 0 |

в) \(𝑥 + 6 𝑦 = 0\);
| \(x\) | 0 | 6 |
| \(y\) | 0 | -1 |

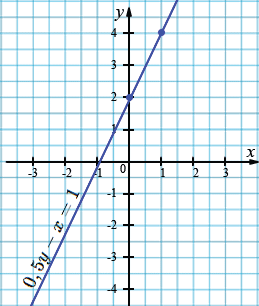
г) \(0,5 𝑦 − 𝑥 = 1\);
| \(x\) | 0 | 1 |
| \(y\) | 2 | 4 |
д) \(1,2 𝑥 = − 4,8\);
\(1,2 𝑥 + 0y= − 4,8\);
\(𝑥 = − 4,8:1,2\);
\(𝑥 = −4.\)

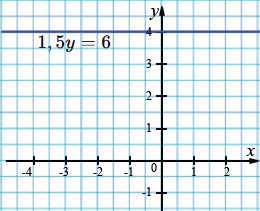
е) \(1,5 𝑦 = 6;\)
\(0x+1,5 𝑦 = 6;\)
\(𝑦 = 6:1,5;\)
\(𝑦 = 4.\)
Пояснения:
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая. Прямая определяется двумя точками, поэтому чтобы построить график линейного уравнения с двумя переменными достаточно определить координаты каких-либо двух точек прямой.
№1064 учебника 2013-2022 (стр. 211):
а) \( \begin{cases} x - 3y = 5, \\ 3x - 9y = 15; \end{cases}\)
\( \begin{cases} -3y = 5 - x, \\ -9y = 15 - 3x; \end{cases}\)
\( \begin{cases} y = \frac{x - 5}{3}, \\ y = \frac{3x - 15}{9}; \end{cases}\)
\( \begin{cases} y = \frac{x - 5}{3}, \\ y =\frac{x - 5}{3}. \end{cases}\)
Уравнения совпадают, значит, система имеет бесконечно много решений.
Если \(x=0\), то \( y = \tfrac{0 - 5}{3}=-1\frac{2}{3};\)
Если \(x=5\), то \( y = \tfrac{5 - 5}{3}=0;\)
Если \(x=2\), то \( y = \tfrac{2 - 5}{3}=-3.\)
Ответ: \((0;-1\tfrac{2}{3})\); \((5; 0)\); \((2;-3)\).
б) \( \begin{cases} 1{,}5y + x = -0{,}5, \\ 2x + 3y = -1; \end{cases} \)
\( \begin{cases} 1{,}5y = -\,0{,}5 - x, \\ 3y = -1 - 2x; \end{cases} \)
\( \begin{cases} y = \frac{-0{,}5 - x}{1{,}5}, \\ y = \frac{-1 - 2x}{3}; \end{cases} \)
\( \begin{cases} y = \frac{-1 - 2x}{3}, \\ y = \frac{-1 - 2x}{3}. \end{cases} \)
Уравнения совпадают, значит, система имеет бесконечно много решений.
Если \(x=0\), то \( y = \tfrac{-1 - 2\cdot0}{3}=-\tfrac13;\)
Если \(x=1\), то \( y = \tfrac{-1 - 2\cdot1}{3}=-1;\)
Если \(x=4\), то \( y = \tfrac{-1 - 2\cdot4}{3}=-3.\)
Ответ: \((0;-\tfrac13)\); \((1; -1)\); \((4;-3)\).
Пояснения:
Метод выражения переменной:
Для уравнения вида \(ax + by = c\) переносим \(ax\) в правую часть: \(by = c - ax\), затем делим на \(b\):
\[ y = \frac{c - ax}{b}. \]
В обеих системах выражения для \(y\) в первом и во втором уравнении совпадают, что соответствует бесконечному множеству решений.
Вернуться к содержанию учебника