Упражнение 1077 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1077 учебника 2023-2025 (стр. 212):
Решите графически систему уравнений:
а) \( \begin{cases} x - 2y = 6, \\ 3x + 2y = -6; \end{cases}\)
б) \( \begin{cases} x - y = 0, \\ 2x + 3y = -5. \end{cases} \)
№1077 учебника 2013-2022 (стр. 214):
Найдите решение системы уравнений:
а) \( \begin{cases} \frac{x}{3} - \frac{y}{2} = -4,\\ \frac{x}{2} + \frac{y}{2} = -2; \end{cases} \)
б) \( \begin{cases} \frac{a}{6} - 2b = 6,\\ -3a + \frac{b}{2} = -37; \end{cases} \)
в) \( \begin{cases} \frac{2m}{5} + \frac{n}{3} = 1,\\ \frac{m}{10} - \frac{7n}{6} = 4; \end{cases} \)
г) \( \begin{cases} 7x - \frac{3y}{5} = -4,\\ x + \frac{2y}{5} = -3. \end{cases} \)
Подсказка
№1077 учебника 2023-2025 (стр. 212):
№1077 учебника 2013-2022 (стр. 214):
Вспомните:
- Что значит решить систему уравнений.
- Способ подстановки при решении систем уравнений.
- Свойства уравнений.
- Линейное уравнение.
- Деление и дроби.
- Деление десятичных дробей.
- Подобные слагаемые.
- Умножение обыкновенных дробей.
- Сокращение дробей.
- Сложение десятичных дробей.
- Приведение дробей к общему знаменателю.
- Распределительное свойство умножения.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение рациональных чисел.
- Деление рациональных чисел.
Ответ
№1077 учебника 2023-2025 (стр. 212):
а) \( \begin{cases} x - 2y = 6, \\ 3x + 2y = -6; \end{cases}\)
\(x - 2y = 6:\)
| \(x\) | 0 | 2 |
| \(y\) | -3 | -2 |
\(3x + 2y = -6:\)
| \(x\) | 0 | -2 |
| \(y\) | -3 | 0 |
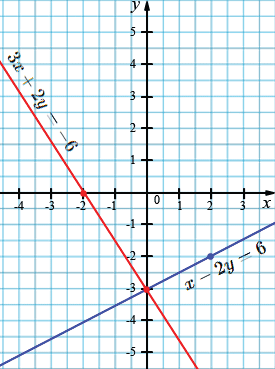
Ответ: \( (0; -3) \)
б) \( \begin{cases} x - y = 0, \\ 2x + 3y = -5. \end{cases} \)
\(x - y = 0:\)
| \(x\) | 0 | 3 |
| \(y\) | 0 | 3 |
\( 2x + 3y = -5:\)
| \(x\) | -1 | 2 |
| \(y\) | -1 | -3 |

Ответ: \( (-1; -1) \)
Пояснения:
Решение системы графически означает построение двух прямых на координатной плоскости и нахождение их точки пересечения (если она существует).
№1077 учебника 2013-2022 (стр. 214):
а) \( \begin{cases} \frac{x}{3} - \frac{y}{2} = -4 /\times 6,\\ \frac{x}{2} + \frac{y}{2} = -2 /\times 2; \end{cases} \)
\( \begin{cases} 2x - 3y = -24,\\ x + y = -4; \end{cases} \)
\( \begin{cases} 2\cdot(-4 - y) - 3y = -24,\\ x = -4 - y; \end{cases} \)
\( 2\cdot(-4 - y) - 3y = -24\)
\(-8 -2y -3y = -24\)
\(-5y = -24+8\)
\(-5y = -16\)
\(y = \tfrac{16}{5}\)
\(y = 3,2\)
\( x = -4 - 3,2 = -7,2. \)
Ответ: \( x = -7,2,\) \(y = 3,2\).
б) \( \begin{cases} \frac{a}{6} - 2b = 6, /\times 6 \\ -3a + \frac{b}{2} = -37; /\times 2 \end{cases} \)
\( \begin{cases} a - 12b = 36, \\ -6a + b = -74;\end{cases} \)
\( \begin{cases} a = 36 + 12b, \\ -6\cdot(36 + 12b) + b = -74;\end{cases} \)
\(-6\cdot(36 + 12b) + b = -74\)
\(-216 -72b + b = -74\)
\(-71b = -74 + 216\)
\(-71b = 142\)
\(b = -\frac{142}{71}\)
\(b = -2\)
\(a = 36 +12\cdot(-2) = 36 - 24 = 12\)
Ответ: \(a = 12\), \(b = -2\).
в) \( \begin{cases} \frac{2m}{5} + \frac{n}{3} = 1, /\times 15 \\ \frac{m}{10} - \frac{7n}{6} = 4; /\times 30 \end{cases} \)
\( \begin{cases} 6m+5n=15,\\ 3m-35n=120; \end{cases} \)
\( \begin{cases} 5n=15-6m,\\ 3m-35n=120; \end{cases} \)
\( \begin{cases} n=\frac{15-6m}{5},\\ 3m-35\cdot\frac{15-6m}{5}=120; \end{cases} \)
\(3m-^7\cancel{35}\cdot\frac{15-6m}{\cancel5}=120\)
\(3m-7\cdot(15-6m)=120\)
\(3m-105+42m=120\)
\(45m=120 + 105\)
\(45m=225\)
\(m=\frac{225}{45}\)
\(m=5\)
\(n=\frac{15-6\cdot5}{5} =\frac{15-30}{5} =\)
\(=\frac{-15}{5}=-3\)
Ответ: \(m=5\), \(n= -3\).
г) \( \begin{cases} 7x - \frac{3y}{5} = -4, /\times 5\\ x + \frac{2y}{5} = -3 /\times 5 \end{cases} \)
\( \begin{cases} 35x - 3y = -20, \\ 5x + 2y = -15 \end{cases} \)
\( \begin{cases} 35x - 3y = -20, \\ 5x = -15 - 2y \end{cases} \)
\( \begin{cases} 35\cdot\frac{-15 - 2y}{5} - 3y = -20, \\ x = \frac{-15 - 2y}{5} \end{cases} \)
\(^7\cancel{35}\cdot\frac{-15 - 2y}{\cancel5} - 3y = -20\)
\(7\cdot(-15 - 2y) -3y=-20\)
\(-105-14y-3y=-20\)
\(-17y=-20 + 105\)
\(-17y=85\)
\(y=-\frac{85}{17}\)
\(y=-5\)
\(x = \frac{-15 - 2\cdot(-5)}{5} =\)
\(=\frac{-15+10}{5}=-\frac{5}{5} = -1\)
Ответ: \(x = -1\), \(y=-5\).
Пояснения:
Метод подстановки:
1. В каждом уравнении избавляемся от дробей, домножив обе части уравнения на общий знаменатель дробей, входящих в уравнение.
2. Из одного уравнения выражаем одну переменную через другую.
3. Подставляем полученное выражение в другое уравнение, сводя систему к одному уравнению с одной переменной.
4. Решаем это уравнение, находим значение первой переменной.
5. Подставляем найденное значение обратно для вычисления второй переменной.
Вернуться к содержанию учебника