Упражнение 1126 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник. Страница 223

Пусть \(x\) (км/ч) скорость автомобиля из \(A\), а \(y\) (км/ч) — скорость автомобиля из \(B\).

Составим систему уравнений:

\( \begin{cases} (x + y)\cdot 2 = 280,\\ (x - y)\cdot 14 = 280. \end{cases} \)

\( \begin{cases} (x + y)\cdot 2 = 280,   / : 2 \\ (x - y)\cdot 14 = 280   / : 14 \end{cases} \)

\( \begin{cases} x + y = 140, \\ x - y = 20   / : 14 \end{cases} \)

\( \begin{cases} x + y = 140, \\ x - y = 20 \end{cases} \)

\( \begin{cases} 2x = 160, \\ x - y = 20 \end{cases} \)

\( \begin{cases} x = \frac{160}{2}, \\ y = x - 20 \end{cases} \)

\( \begin{cases} x = 80, \\ y = 80 - 20 \end{cases} \)

\( \begin{cases} x = 80, \\ y = 60 \end{cases} \)

Ответ: скорости автомобилей \(80\) км/ч из \(A\) и \(60\) км/ч из \(B\).

Пояснения:

Использованные приёмы:

1) Введение переменных: \(x\) и \(y\) для скоростей двух автомобилей.

2) Составление системы по двум ситуациям:

– навстречу друг другу расстояние 280 км преодолевают за 2 ч:

\((x+y)\cdot2=280\);

– в одном направлении автомобиль из \(A\) догоняет автомобиль из \(B\) за 14 ч при начальном разрыве 280 км:

\((x-y)\cdot14=280\).

3) Решение системы методом сложения: складываем почленно уравнения системы так, чтобы в новом уравнении исчезла одна из переменных. После сложения уравнений системы получается линейное уравнение с одной переменной, решение которого дает значение этой переменной. Там, где необходимо, одно из уравнений или оба уравнения делим или умножаем на числа так, чтобы перед одной из переменных получить противоположные коэффициенты, которые при сложении приведут к сокращению выражений с этой переменной.

4) Уравнение вида \(ax = b\) называется линейным и при \(a \neq 0\) имеет единственный корень \(x=\frac{b}{a}\).

5) Подстановка: после нахождения одной переменной подставляем её значение в одно из исходных уравнений для вычисления значения второй переменной.

а)  \(2x + 5y = 12\)

\( 5y = 12 - 2x \)

\(y = \frac{12 - 2x}{5} \)

\(y = \frac{12}{5} - \frac{2}{5}x \)

\(y = 2,4 - 0,4x \)

\(y = -0,4x + 2,4 \)

\(k < 0\), \(b > 0\), значит, график расположен в I, II и IV координатной четвертях.

Ответ: I, II и IV координатные четверти.

б)  \(3x - 4y = 10\)

\( -4y = 10 - 3x \)

\( y = \frac{3x - 10}{4} \)

\( y = \frac{3}{4}x - \frac{10}{4} \)

\( y = 0,75x - 2,5 \)

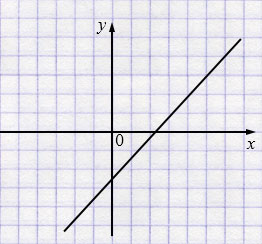
\(k > 0\), \(b < 0\), значит, график расположен в I, III и IV координатной четвертях.

Ответ: I, III и IV координатные четверти.

Пояснения:

Использованные приёмы:

Для каждой прямой выразили \(y\) через \(x\),то есть получили уравнение линейной функции вида \(y = kx + b\) и определили знаки коэффициентов \(k\) и \(b\), которые отвечают за расположение прямой на координатной плоскости.

Коэффициент \(k\) отвечает за возрастание (когда \(k > 0\)) или убывание (когда \(k < 0\)) линейной функции.

Коэффициент \(b\) отвечает за точку пересечения с осью \(y\), если \(b > 0\), то прямая пересекает ось \(y\) выше оси \(x\), а если \(b < 0\), то прямая пересекает ось \(y\) ниже оси \(x\).

а)

б)