Упражнение 983 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

а) \(y=\dfrac{x-2}{\sqrt{x+6}-\sqrt{2x-5}}\)

\(\begin{cases} x+6\ge 0,\\ 2x-5\ge 0,\\ \sqrt{x+6}-\sqrt{2x-5}\ne 0 \end{cases}\)

\(\begin{cases} x\ge -6,\\ 2x\ge 5,   / : 5 \\ \sqrt{x+6}\neq\sqrt{2x-5} \end{cases}\)

\(\begin{cases} x\ge -6,\\ x\ge 2,5, \\ x+6\neq2x-5 \end{cases}\)

\(\begin{cases} x\ge -6,\\ x\ge 2,5, \\ x-2x\neq-5-6 \end{cases}\)

\(\begin{cases} x\ge -6,\\ x\ge 2,5, \\ -x\neq-11  /\times(-1) \end{cases}\)

\(\begin{cases} x\ge -6,\\ x\ge 2,5, \\ x\neq11 \end{cases}\)

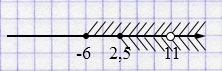
Ответ: \(x \in [2,5; 11) \cup (11; +\infty )\).

б) \(y=\dfrac{6}{\sqrt{2x-1}-\sqrt{x+1}}\)

\(\begin{cases} 2x-1\ge 0,\\ x+1\ge 0,\\ \sqrt{2x-1}-\sqrt{x+1}\ne 0 \end{cases}\)

\(\begin{cases} 2x\ge 1,  / : 2 \\ x\ge -1,\\ \sqrt{2x-1}\neq\sqrt{x+1} \end{cases}\)

\(\begin{cases} x\ge 0,5, \\ x\ge -1,\\ 2x-1\neq x+1 \end{cases}\)

\(\begin{cases} x\ge 0,5, \\ x\ge -1,\\ 2x-x\neq 1+1 \end{cases}\)

\(\begin{cases} x\ge 0,5, \\ x\ge -1,\\ x\neq 2 \end{cases}\)

Ответ: \(x \in [0,5; 2) \cup (2; + \infty )\).

Пояснения:

Для выражений с квадратным корнем необходимо выполнение условия: подкоренное выражение неотрицательно. Также у рациональных дробей знаменатель должен быть отличен от нуля.

Поэтому каждое выражение преобразуется в систему, состоящую из двух неравенств и уравнения. Решение системы даёт допустимые значения переменной.

Чтобы решить систему неравенств, нужно найти пересечение решений неравенств системы, то есть найти множество чисел, которое является одновременно решением и одного неравенства и решением другого неравенства. Если решения неравенств не пересекаются, то система решений не имеет.

При решении неравенств системы используем то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства разделить на одно и то же положительное число, то получится равносильное ему неравенство;

- если обе части неравенства разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.

При решении уравнений корни переносим в разные части уравнения и возводим каждую часть уравнения в квадрат,учитывая то, что

\((\sqrt a)^2 = a\).

\(\dfrac{(n - 7)^2}{n} =\dfrac{n^2 - 14 n +49}{n}= \)

\(=\dfrac{n^2}{n} - \dfrac{14n}{n} + \dfrac{49}{n}=\)

\(=n - 14 + \dfrac{49}{n}\)

Натуральные делители \(49\):

\(1, 7, 49\).

Если \( n = 1\), то

\(1 - 14 + \dfrac{49}{1} = -13 + 49 = 36\) - натуральное число.

Если \( n = 7\), то

\(7 - 14 + \dfrac{49}{7} = -7 + 7 = 0\) - не является натуральным числом.

Если \( n = 49\), то

\(49 - 14 + \dfrac{49}{49} = 35 + 1 = 36\) - натуральное число.

Ответ: при \(n = 1\) и \(n = 49.\)

Пояснения:

Чтобы дробь \(\dfrac{(n - 7)^2}{n}\) была натуральным числом, числитель \((n - 7)^2\) должен делиться на \(n\) без остатка.

Так как \((n - 7)^2 = n^2 - 14n + 49\), то остаток от деления на \(n\) равен остатку от деления 49 на \(n\).

Следовательно, чтобы дробь \(\dfrac{(n - 7)^2}{n} \) принимала натуральные значения \(49\) должно делиться на \(n\).

Натуральные делители числа 49 — это 1, 7, 49.

Выполнив проверку, получаем, что при \(n = 1\) и \(n = 49\) дробь \(\dfrac{(n - 7)^2}{n} \) принимает натуральные значения.