Упражнение 1171 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 260
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№1171 учебника 2023-2025 (стр. 260):
В одной системе координат постройте графики функций и найдите координаты их точек пересечения:
а) \(y = -\dfrac{1}{x}\) и \(y = -x\);
б) \(y = \dfrac{2}{x}\) и \(y = x + 1.\)
Подсказка
№1171 учебника 2023-2025 (стр. 260):
Вспомните:
- Функцию обратной пропорциональности, ее график.
- Деление и дроби.
- Деление десятичных дробей.
- Деление рациональных чисел.
- Линейную функцию, ее график.
- Координаты точки на координатной плоскости.
Ответ
№1171 учебника 2023-2025 (стр. 260):
а) \(y = -\dfrac{1}{x}\)
| \(x\) | 0,25 | 0,5 | 1 | 2 | 4 |
| \(y\) | 4 | 2 | 1 | 0,5 | 0,25 |
| \(x\) | -0,25 | -0,5 | -1 | -2 | -4 |
| \(y\) | -4 | -2 | -1 | -0,5 | -0,25 |
\(y = -x\)
| \(x\) | 0 | 3 |
| \(y\) | 0 | -3 |
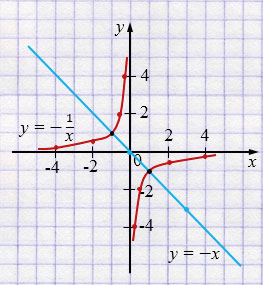
Ответ: точки пересечения \((1; -1)\) и \((-1; 1)\).
б) \(y = \dfrac{2}{x}\)
| \(x\) | 0,5 | 1 | 2 | 4 |
| \(y\) | 4 | 2 | 1 | 0,5 |
| \(x\) | -0,5 | -1 | -2 | -4 |
| \(y\) | -4 | -2 | -1 | -0,5 |
\(y = x + 1\)
| \(x\) | 0 | 3 |
| \(y\) | 1 | 4 |
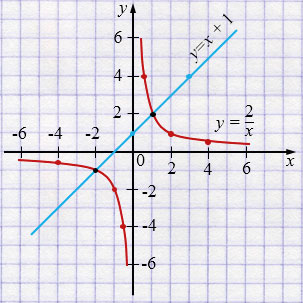
Ответ: точки пересечения \((1; 2)\) и \((-2; -1)\).
Пояснения:
а) Графиком функции \(y = -\dfrac{1}{x}\) является гипербола, ветви которой расположены во 2 и 4 координатных четвертях, так как \(k= -1 < 0\). Строим график по точкам, учитывая то, что \(x \ne 0\).
Графиком функции \(y = -x\) является прямая, проходящая через начало координат. Строим прямую по двум точкам.
Точки пересечения графиков:
\((1; -1)\) и \((-1; 1)\).
б) Графиком функции \(y = \dfrac{2}{x}\) является гипербола, ветви которой расположены во 1 и 3 координатных четвертях, так как \(k= 2 > 0\). Строим график по точкам, учитывая то, что \(x \ne 0\).
Графиком функции \(y = x + 1\) является прямая. Строим прямую по двум точкам.
Точки пересечения графиков:
\((1; 2)\) и \((-2; -1)\).
Вернуться к содержанию учебника