Упражнение 1249 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 279
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№1249 учебника 2023-2025 (стр. 279):
Постройте график функции
\[ y = \begin{cases} x^{-2}, \;если\; -2 \le x < -1,\\[3mm] x^{2}, \;если\; -1 \le x \le 1,\\[3mm] x^{-2}, \;если\; 1 < x \le 2. \end{cases} \]
Сколько общих точек имеет этот график с прямой \(y = a\) в случае, когда:
а) \(a = 2\);
б) \(a = 1\);
в) \(a = \dfrac{1}{2}\);
г) \(a = 0\)?
Подсказка
№1249 учебника 2023-2025 (стр. 279):
Вспомните:
- График функции \(y=x^{-2}\).
- Степень с целым отрицательным показателем.
- Степень с натуральным показателем.
- Деление и дроби.
- Деление десятичных дробей.
- Координаты точки на координатной плоскости.
- Квадратичная функция, ее график.
- Числовые промежутки.
- Линейная функция, ее график.
- Параллельные прямые.
Ответ
№1249 учебника 2023-2025 (стр. 279):
\[ y = \begin{cases} x^{-2}, \;если\; -2 \le x < -1,\\[3mm] x^{2}, \;если\; -1 \le x \le 1,\\[3mm] x^{-2}, \;если\; 1 < x \le 2. \end{cases} \]
\(y = x^{-2} = \frac{1}{x^2}\), \(-2 \le x < -1\)
| \(x\) | -2 | -1 |
| \(y\) | 0,25 | 1 |
\(y = x^{2} \), \(-1 \le x \le 1\)
| \(x\) | -1 | 0 | 1 |
| \(y\) | 1 | 0 | 1 |
\(y = x^{-2} = \frac{1}{x^2}\), \(1 < x \le 2\)
| \(x\) | 1 | 2 |
| \(y\) | 1 | 0,25 |
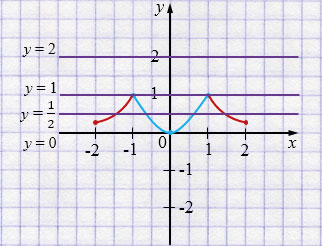
\(y = a\) - прямая, параллельная оси \(x\).
а) Если \(a = 2\), то общих точек нет.
б) Если \(a = 1\), то 2 общих точки.
в) Если \(a = \dfrac{1}{2}\), то 4 общих точки.
г) Если \(a = 0\), то 1 общая точка.
Пояснения:
Построить нужно кусочную функцию, которая состоит из трех частей:
1) \(y = x^{-2}\) при \(-2 \le x < -1\);
2) \(y = x^{2}\) при \(-1 \le x \le 1\);
3) \(y = x^{-2}\) при \(1 < x \le 2\).
\(y = a\) - это прямая, параллельная оси \(x\). Построив в той же системе координат, что и график кусочной функции прямые \(y = a\) при заданном значении \(a\), определяем количество общих точек этих графиков.
Вернуться к содержанию учебника