Упражнение 1244 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 278
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№1244 учебника 2023-2025 (стр. 278):
Постройте график функции \[ y=\begin{cases} x, & \text{если } x\le 0,\\ x^{-1}, & \text{если } x>0. \end{cases} \] Найдите:
а) значение \(y\), если \(x=-2;\;2\);
б) значение \(x\), при котором \(y=-4;\;4\).
Подсказка
№1244 учебника 2023-2025 (стр. 278):
Вспомните:
- Линейную функцию, ее график.
- Функцию обратной пропорциональности, ее график.
- Координаты точки на координатной плоскости.
- Степень с целым отрицательным показателем.
- Деление и дроби.
- Деление десятичных дробей.
Ответ
№1244 учебника 2023-2025 (стр. 278):
\[ y=\begin{cases} x, & \text{если } x\le 0,\\ x^{-1}, & \text{если } x>0. \end{cases} \]
\(y = x\), \(x\ge0\)
| \(x\) | 0 | -3 |
| \(y\) | 0 | -3 |
\(y = x^{-1} = \frac1x\), \(x>0\)
| \(x\) | 0,25 | 0,5 | 1 | 2 | 4 |
| \(y\) | 4 | 2 | 1 | 0,5 | 0,25 |
а) Если \(x=-2\le 0\), то
\(y=-2\).
Если \( x=2>0\), то
\(y=2^{-1}=\dfrac{1}{2} = 0,5.\)
б) Если \(y=-4\), то
\(x=-4\) .
Если \(y=4\), то
\(4=x^{-1}\)
\(4= \frac1x\)
\( x =\dfrac14 = 0,25\).
Пояснения:
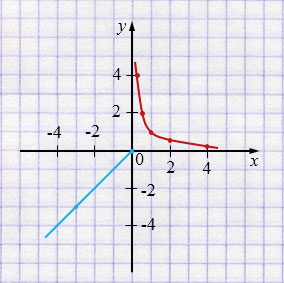
Функция кусочная: для \(x\le 0\) это прямая \(y=x\) (берём часть слева от нуля включительно, точка \((0,0)\) входит); для \(x>0\) — ветвь гиперболы \(y=\dfrac1x\) в первой четверти (ноль в область не входит).
Для вычисления значения функции выбираем ветвь по условию на \(x\):
если \(x\le 0\), то \(y=x\);
если \(x>0\), то \(y=x^{-1}\).
Чтобы найти \(x\) по заданному \(y\), решаем уравнения отдельно по ветвям. Чтобы понять в какую функцию \(y = x\) или \(y = x^{-1}\) подставлять значение \(y\), обращаемся к графику.
Вернуться к содержанию учебника