Упражнение 1245 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 278
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№1245 учебника 2023-2025 (стр. 278):
Постройте график функции \(y = |x^{-1}|\). Как расположен этот график относительно оси \(y\)?
Подсказка
№1245 учебника 2023-2025 (стр. 278):
Вспомните:
- График обратной пропорциональности.
- Положение точек на координатной плоскости.
- Деление и дроби.
- Деление десятичных дробей.
- Противоположные числа.
- Модуль числа.
Ответ
№1245 учебника 2023-2025 (стр. 278):
\( y = |x^{-1}| = |\frac1x|\)
\( y = \begin{cases} \dfrac{1}{x}, & \text{если } x > 0,\\[3mm] -\dfrac{1}{x}, & \text{если } x < 0. \end{cases} \)
\(y=\dfrac{1}{x}\), \(x > 0\)
| \(x\) | 4 | 2 | 1 | 0,5 | 0,25 |
| \(y\) | 0,25 | 0,5 | 1 | 2 | 4 |
\(y=-\dfrac{1}{x}\), \(x < 0\)
| \(x\) | -0,25 | -0,5 | -1 | -2 | -4 |
| \(y\) | 4 | 2 | 1 | -0,5 | 0,25 |
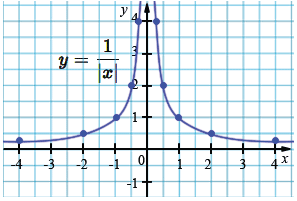
График симметричен относительно оси \(y\).
Пояснения:
Гипербола \(y = x^{-1}\) имеет ветви в I и III четвертях. При взятии модуля отрицательные значения \(y\) становятся положительными. Поэтому ветвь из III четверти «отражается» вверх — в II четверть. График функции \(y = |x^{-1}|\) имеет две симметричные ветви, расположенные в I и II четвертях. Точки на оси \(y\) график не имеет, так как функция не определена при \(x = 0\).
Вернуться к содержанию учебника