Упражнение 1321 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 286

\( \begin{cases} x(x - 2) = y + 12x,\\ xy - 5 = 0 \end{cases} \)

\( \begin{cases} x^2 - 2x = y + 12x,\\ xy = 5 \end{cases} \)

\( \begin{cases} y = x^2 - 2x  - 12x,\\ y = \frac5x \end{cases} \)

\( \begin{cases} y = x^2 - 14x,\\ y = \frac5x \end{cases} \)

\(y = x^2 - 14x \) - парабола, ветви которой направлены вверх.

\(x^2 - 14x = 0\)

\(x(x-14)=0\)

\(x= 0\)  или  \(x -14 =0\)

                    \(x = 14\)

\((0;0)\) и \((14;0)\) - точки пересечения параболы с осью \(x\).

\(y = \frac5x\) - гипербола, ветви лежат в 1 и 3 координатных четвертях.

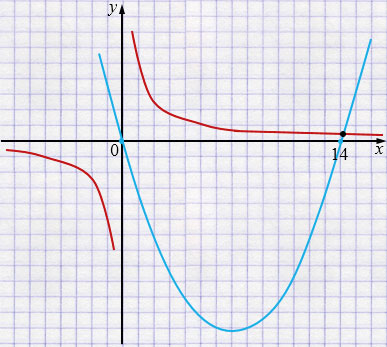
Ответ: одно решение.

Пояснения:

Используем графический метод при решении системы уравнений. Графики строим схематично, так как количеству решений системы соответствует количеству точек пересечения графиков уравнений, входящих в систему.

Из первого уравнения \(x(x - 2) = y + 12x\), получаем квадратичную функцию \(y = x^2 - 14x\), графиком которой является парабола, ее ветви направлены вверх, так как коэффициент перед \(x^2\) положительный, и график пересекает ось \(x\) в двух точках \((0;0)\) и \((14;0)\).
Из второго уравнения \(xy - 5 = 0\), получаем функцию обратной пропорциональности \(y = \frac5x\), графиком которой является гипербола с ветвями расположенными в 1 и 3 координатных четвертях, так как коэффициент \(k=5 > 0\).

Графики полученных функций пересекаются в одной точке, значит, система уравнений имеет одно решение.