Упражнение 1323 - ГДЗ по Алгебре 8 класс Макарычев, Миндюк учебник

№1323 учебника 2023-2025 (стр. 287):

Решите графическим способом систему уравнений:

а) \( \begin{cases} y - x^2 = -1,\\ y - 2x = 1; \end{cases} \)

б) \( \begin{cases} xy - 1 = 0,\\ y + x^2 = 3. \end{cases} \)

№1323 учебника 2023-2025 (стр. 287):

Вспомните:

№1323 учебника 2023-2025 (стр. 287):

а) \( \begin{cases} y - x^2 = -1,\\ y - 2x = 1; \end{cases} \)

\( \begin{cases} y = x^2 -1,\\ y = 2x + 1; \end{cases} \)

\(y = x^2 - 1\) - парабола, ветви которой направлены вверх.

\(x\)	\(-3\)	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(3\)
\(y\)	\(8\)	\(3\)	\(0\)	\(-1\)	\(0\)	\(3\)	\(8\)

\(y = 2x + 1\) - прямая.

\(x\)	\(0\)	\(2\)
\(y\)	\(1\)	\(5\)

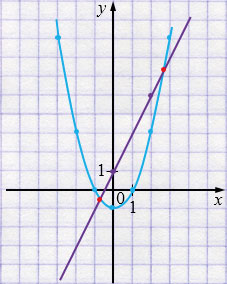
Ответ: \((-0,7; -0,5)\) и \((2,7; 6,5)\).

б) \( \begin{cases} xy - 1 = 0,\\ y + x^2 = 3. \end{cases} \)

\( \begin{cases} xy = 1,\\ y = - x^2 + 3 \end{cases} \)

\( \begin{cases} y = \frac1x,\\ y = - x^2 + 3 \end{cases} \)

\(y = \frac1x\) - гипербола, ветви которой расположены в 1 и 3 координатных четвертях.

\(x\)	\(0,5\)	\(1\)	\(2\)
\(y\)	\(2\)	\(1\)	\(0,5\)

\(x\)	\(-2\)	\(-1\)	\(-0,5\)
\(y\)	\(-0,5\)	\(-1\)	\(-2\)

\(y = - x^2 + 3\) - парабола, ветви которой направлены вниз.

\(x\)	\(-3\)	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(3\)
\(y\)	\(-6\)	\(-1\)	\(2\)	\(3\)	\(2\)	\(-1\)	\(-6\)

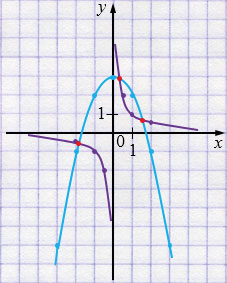
Ответ: \((-1,9; -0,5)\), \((0,4; 2,9)\) и \((1,6;0,6)\).

Пояснения:

Суть графического метода решения системы уравнений с двумя переменными:

1) построить на одной координатной плоскости графики уравнений, входящих в систему;

2) найти координаты всех точек пересечения построенных графиков;

3) полученные пары чисел и будут искомыми решениями.

Решения систем уравнений найдены приближенно, так как координаты точек можем определить только приближенно.

Упражнение 1323 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 287