Упражнение 177 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник

\(g(x)=\dfrac{6}{|x-2|}\)

Асимптоты: \(x = 2\) и \(y = 0\).

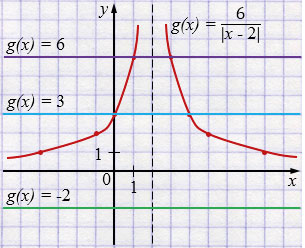
а) \(g(x)=3\)

Ответ: \(x = 0\)  и  \(x = 4\).

б) \(g(x)=6\)

Ответ: \(x = 1\)  и  \(x = 3\).

в) \(g(x)=-2\)

Ответ: решений нет.

Пояснения:

Модуль удовлетворяет равенству \(|A|=k\) при \(k>0\), если \(A=k\) или \(A=-k\).

Функция \(\dfrac{6}{|x-2|}\) всегда положительна, так как числитель положителен, а модуль неотрицателен.

\(g(x)=\dfrac{6}{|x-2|}\) - функция имеет вертикальную асимптоту \(x=2\) и горизонтальную асимптоту \(y=0\). Поэтому график — гипербола \(y=\dfrac{6}{x}\), сдвинутая вправо на \(2\) единицы и отрицательная ветвь которой симметрично отражена относительно оси \(x\). Для построения графика функции пунктиром проводим асимптоту: прямую \(x = 2\). Так как гипербола состоит из двух ветвей, составляем две таблицы: одну для \(x < 2\), другую для \(x > 2\). Отметив точки в координатной плоскости, координаты которых указаны в первой таблице, и соединив их плавной непрерывной линией, получим одну ветвь гиперболы. Аналогично, используя вторую таблицу, получим вторую ветвь гиперболы.

Чтобы решить уравнения вида \(g(x) = k\), нужно найти точки пересечения графиков \(g(x)=\dfrac{6}{|x-2|}\) и \(g(x) = k\), абсциссы (координаты \(x\)) этих точек являются корнем рассматриваемого уравнения.

\(g(x) = k\) - прямая, параллельная оси \(x\), проходящая через точку \((0; k)\).

а) \(y=(x-2)^2\) - парабола, ветви вверх.

вершина: \((2;0)\)

б) \(y=-\dfrac{1}{2}x^2+5\) - парабола, ветви вниз.

вершина: \((0;5)\)

в) \(y=2x^2+5x\) - парабола, ветви вверх.

\(x_0=-\dfrac{b}{2a}=-\dfrac{5}{4} = -1,25\)

\(y_0=2\cdot(-1,25)^2+5\cdot(-1,25)=\)

\(=3,125 - 6,25 =-3,125 \)

вершина: \((-1,25;-3,125)\)

Пояснения:

Все функции являются квадратичными, их график — парабола.

Общий вид квадратичной функции:

\[ y=ax^2+bx+c \]

Основные элементы:

\((x_0; y_0)\) - вершина параболы.

\[ x_0=-\frac{b}{2a}, \]

\[ y_0=f(x_0) .\]

При \(a > 0\) ветви параболы направленны вверх, при \(a < 0\) - вниз.