Упражнение 180 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 68

а) \(f(x)=kx+b\),

\(k>0,\; b>0\)

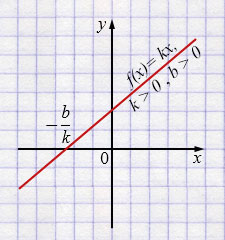
Свойства:

1. \(D(f) = (-\infty; + \infty)\).

2. \(E(f) = (-\infty; + \infty)\).

3. \(f(x) = 0\) при \(x = -\frac{b}{k}\).

4. \(f(x) > 0\) при \(x > -\frac{b}{k}\),

\(f(x) < 0\) при \(x < -\frac{b}{k}\).

5. Функция возрастает на \((-\infty; + \infty)\).

6. Наибольшего и наименьшего значений функция не имеет.

7. Функция не является ни четной и ни нечетной.

б) \(f(x)=kx+b\)

\(k<0,\; b<0\)

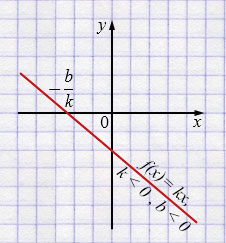
Свойства:

1. \(D(f) = (-\infty; + \infty)\).

2. \(E(f) = (-\infty; + \infty)\).

3. \(f(x) = 0\) при \(x = -\frac{b}{k}\).

4. \(f(x) > 0\) при \(x < -\frac{b}{k}\),

\(f(x) < 0\) при \(x > -\frac{b}{k}\).

5. Функция убывает на \((-\infty; + \infty)\).

6. Наибольшего и наименьшего значений функция не имеет.

7. Функция не является ни четной и ни нечетной.

в) \(f(x)=kx+b\)

\(k>0,\; b<0\)

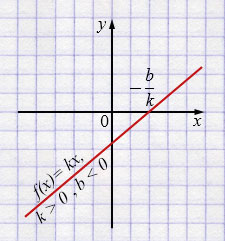
Свойства:

1. \(D(f) = (-\infty; + \infty)\).

2. \(E(f) = (-\infty; + \infty)\).

3. \(f(x) = 0\) при \(x = -\frac{b}{k}\).

4. \(f(x) > 0\) при \(x > -\frac{b}{k}\),

\(f(x) < 0\) при \(x < -\frac{b}{k}\).

5. Функция возрастает на \((-\infty; + \infty)\).

6. Наибольшего и наименьшего значений функция не имеет.

7. Функция не является ни четной и ни нечетной.

Пояснения:

1. Функция \(f(x)=kx+b\) — это прямая. Знак коэффициента \(k\) определяет направление:

— если \(k>0\) — прямая возрастает;

— если \(k<0\) — прямая убывает.

2. Коэффициент \(b\) задаёт точку пересечения с осью \(y\):

— \(b>0\) — выше оси;

— \(b<0\) — ниже оси.

3. Нуль функции находится из уравнения \(kx+b=0\):

\[ x = -\frac{b}{k}. \]

От его знака зависит положение точки пересечения графика с осью \(x\).