Упражнение 179 - ГДЗ по Алгебре 9 класс Макарычев, Миндюк учебник. Страница 68

Постройте в одной и той же системе координат графики функций:

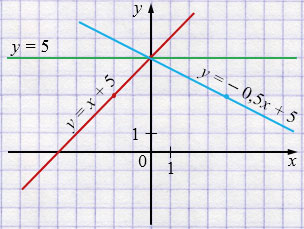
а) \(y=x+5;\; y=-0{,}5x+5;\; y=5;\)

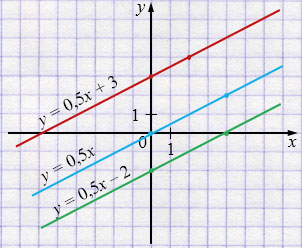
б) \(y=0{,}5x+3;\; y=0{,}5x;\; y=0{,}5x-2.\)

Вспомните:

а) 1) \(y=x+5\)

\(x\)	\(0\)	\(-2\)
\(y\)	\(5\)	\(3\)

2) \(y=-0{,}5x+5\)

\(x\)	\(0\)	\(4\)
\(y\)	\(5\)	\(3\)

3) \(y=5\) — горизонтальная прямая.

б) 1) \(y=0{,}5x+3\)

\(x\)	\(0\)	\(2\)
\(y\)	\(3\)	\(4\)

2) \(y=0{,}5x\)

\(x\)	\(0\)	\(4\)
\(y\)	\(0\)	\(2\)

3) \(y=0{,}5x-2\)

\(x\)	\(0\)	\(4\)
\(y\)	\(-2\)	\(0\)

Пояснения:

Правила построения линейных функций:

— любая функция вида \(y=kx+b\) строится по двум точкам;

— если \(k<0\), прямая убывает; если \(k>0\), возрастает; если \(k=0\), прямая горизонтальная (параллельная оси \(x\));

— коэффициент \(b\) показывает точку пересечения прямой с осью \(y\).

Упражнение 179 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 68