Упражнение 184 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 68

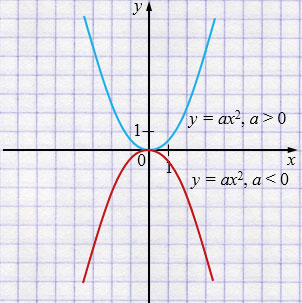
1) Свойства функции \(y = ax^2\), для случая \(a > 0\):

1. \(D(f) = (-\infty; + \infty)\).

2. \(E(f) = [0; +\infty]\).

3. \(y = 0\) при \(x = 0\).

4. \(y > 0\) при \(x \ne 0\).

5. Функция убывает на \((-\infty;0]\) и возрастает на \([0; + \infty)\).

6. Наименьшее значение функции равно нулю при \(x = 0\).

7. Функция является четной.

2) Свойства функции \(y = ax^2\), для случая \(a < 0\):

1. \(D(f) = (-\infty; + \infty)\).

2. \(E(f) = (-\infty; 0]\).

3. \(y = 0\) при \(x = 0\).

4. \(y < 0\) при \(x \ne 0\).

5. Функция возрастает на \((-\infty;0]\) и убывает на \([0; + \infty)\).

6. Наибольшее значение функции равно нулю при \(x = 0\).

7. Функция является четной.

Пояснения:

Функция \(y = ax^{2}\) — парабола, и знак коэффициента \(a\) определяет направление ветвей:

— \(a>0\) — ветви направлены вверх;

— \(a<0\) — ветви направлены вниз.