Упражнение 182 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 68
Вернуться к содержанию учебника
Вопрос
Постройте график функции \(y=\sqrt{kx}\) при \(k\), равном: а) \(2\); б) \(0{,}5\). Как меняется характер графика в зависимости от коэффициента \(k\)?
Подсказка
Вспомните:
Ответ
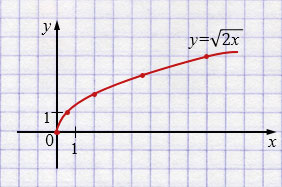
а) \(y=\sqrt{kx}\)
Если \(k=2\), то
\( y=\sqrt{2x}\)
| \(x\) | \(0\) | \(0,5\) | \(2\) | \(4,5\) | \(8\) |
| \(y\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) |
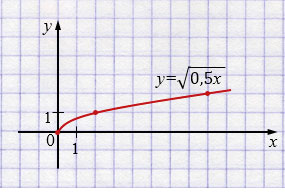
б) \(y=\sqrt{kx}\)
Если \(k=0,5\), то
\( y=\sqrt{0,5x}\)
| \(x\) | \(0\) | \(2\) | \(8\) |
| \(y\) | \(0\) | \(1\) | \(2\) |
Характер графика:
— при \(k>1\) график растягивается по вертикали (отдаляется от оси \(x\));
— при \(0 < k < 0\) график сжимается по вертикали (прижимается к оси \(x\)).
Пояснения:
График функции \(y=\sqrt{x}\) — стандартная функция. Умножение подкоренного выражения на коэффициент \(k\) эквивалентно домножению всего результата на \(\sqrt{k}\). Поэтому при построении достаточно умножить ординаты стандартной функции \(y=\sqrt{x}\) на число \(\sqrt{k}\). Увеличение коэффициента \(k\) «поднимает» график, уменьшение — «опускает» его.
Вернуться к содержанию учебника