стр. 139 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник
Вернуться к содержанию учебника
Контрольные вопросы и задания
Вопрос
1) Что называется решением неравенства с двумя переменными?
2) Какую пару чисел называют решением системы неравенств с двумя переменными?
3) Изобразите на координатной плоскости множество решений неравенства:
а) \(x + y \ge 4\);
б) \(xy \ge 4\).
4) Изобразите на координатной плоскости множество решений системы неравенств \[ \begin{cases} x^2 + y^2 \le 36,\\ x + y \le 6. \end{cases} \]
Подсказка
Ответ
1) Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое равенство
2) Решением системы неравенств с двумя переменными называют такую пару чисел, при подстановке которой каждое неравенство системы превращается в верное числовое неравенство, то есть выполняются все неравенства одновременно.
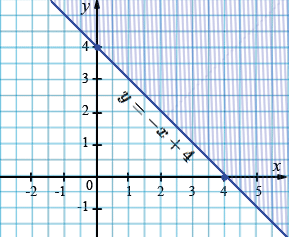
3) а) \(x + y \ge 4\)
\(y \ge -x+4\)
\(y = - x+4\)
| \(x\) | 0 | 4 |
| \(y\) | 4 | 0 |
б) \(xy \ge 4\)
\(y \ge \frac{4}{x}\), \(x\ne0\)
Граница множества решений — гипербола
\( y = \frac{4}{x} \)
| \(x\) | 0,5 | 1 | 2 | 4 | 8 | 0,5 | 1 | 2 | 4 | 8 |
| \(y\) | 8 | 4 | 2 | 1 | 0,5 | 8 | 4 | 2 | 1 | 0,5 |

\((2; 4):\) \(2\cdot4\ge 4\) - верно.
\((0; -2):\) \(0\cdot(-2) \ge 4\) - неверно.
\((-2; -4):\) \((-2)\cdot(-4) \ge 4\) - верно
4) \( \begin{cases} x^2 + y^2 \le 36,\\ x + y \le 6 \end{cases} \)
\( \begin{cases} x^2 + y^2 \le 36,\\ y \le -x+6 \end{cases} \)
\(x^2 + y^2 = 36\) - уравнение окружности с центром в точке \((0; 0)\), радиусом \(r=6.\)
\(y = -x+6\)
| \(x\) | 0 | 6 |
| \(y\) | 6 | 0 |

Вернуться к содержанию учебника