Упражнение 404 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 96
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№404 учебника 2023-2025 (стр. 96):
Какие из выражений не имеют смысла:
а) \(\sqrt{2\sqrt{17}-4}\);
б) \(\sqrt{9-\sqrt{80}}\);
в) \(\sqrt{8\sqrt{3}-14}\);
г) \(\sqrt{15-2\sqrt{56}}\);
д) \(\sqrt{\sqrt{11}-3\sqrt{2}}\);
е) \(\sqrt{2\sqrt{2}-\sqrt{7}}\);
ж) \(\sqrt{6\sqrt{3}-7\sqrt{2}}\);
з) \(\sqrt{ \sqrt{186}-5\sqrt{13}}\);
и) \(\sqrt{ -\sqrt{186}+5\sqrt{7}}\);
к) \(\sqrt{ \sqrt{56}-4\sqrt{2}}\);
л) \(\sqrt{ \sqrt{ 42}-6\sqrt{5}}\);
м) \(\sqrt{ \sqrt{72}-6\sqrt{2}}\).
№404 учебника 2013-2022 (стр. 96):
Вычислите:
а) \(\sqrt{2304}\);
б) \(\sqrt{18225}\);
в) \(\sqrt{254016}\).
Подсказка
№404 учебника 2023-2025 (стр. 96):
Вспомните:
- Что называют арифметическим квадратным корнем.
- Свойства арифметического квадратного корня.
- Внесение множителя под знак корня.
- Степень с натуральным показателем.
№404 учебника 2013-2022 (стр. 96):
Вспомните:
- Что называют арифметическим квадратным корнем.
- Свойства арифметического квадратного корня.
- Модуль числа.
- Степень с натуральным показателем.
- Свойства степени с натуральным показателем.
- Разложение на простые множители.
- Признаки делимости на 2 и на 5.
- Признак делимости на 3.
Ответ
№404 учебника 2023-2025 (стр. 96):
а) \(\sqrt{2\sqrt{17}-4}\) - имеет смысл.
\(2\sqrt{17}-4 =\sqrt{2^2\cdot17}-\sqrt{16}= \)
\(=\sqrt{4\cdot17}-\sqrt{16} = \sqrt{68}-\sqrt{16} > 0\)
б) \(\sqrt{9-\sqrt{80}}\) - имеет смысл.
\(9-\sqrt{80} =\sqrt{81} - \sqrt{80} > 0 \).
в) \(\sqrt{8\sqrt{3}-14}\) - не имеет смысла.
\(8\sqrt{3}-14 = \sqrt{8^2\cdot 3} - \sqrt{196}=\)
\(=\sqrt{64\cdot 3} - \sqrt{196} = \)
\(=\sqrt{192} - \sqrt{196} < 0\).
г) \(\sqrt{15-2\sqrt{56}}\) - имеет смысл.
\(15-2\sqrt{56} = \sqrt{225} - \sqrt{2^2\cdot56}=\)
\(=\sqrt{225} - \sqrt{4\cdot56}=\)
\(=\sqrt{225}-\sqrt{224}>0\).
д) \(\sqrt{\sqrt{11}-3\sqrt{2}}\) - не имеет смысла.
\(\sqrt{11}-3\sqrt{2}=\sqrt{11} - \sqrt{3^2\cdot2}=\)
\(=\sqrt{11} - \sqrt{9\cdot2}=\sqrt{11} - \sqrt{18} < 0\).
е) \(\sqrt{2\sqrt{2}-\sqrt{7}}\) - имеет смысл.
\(2\sqrt{2}-\sqrt{7} = \sqrt{2^2 \cdot 2} - \sqrt{7}=\)
\(=\sqrt{4\cdot2} - \sqrt{7} = \sqrt{8}-\sqrt{7}>0\).
ж) \(\sqrt{6\sqrt{3}-7\sqrt{2}}\) - имеет смысл.
\(6\sqrt{3}-7\sqrt{2} =\sqrt{6^2\cdot3} - \sqrt{7^2\cdot2}= \)
\(=\sqrt{36\cdot3} - \sqrt{49\cdot2} =\)
\(=\sqrt{208} - \sqrt{98}>0\).
з) \(\sqrt{ \sqrt{186}-5\sqrt{13}}\) - не имеет смысла.
\(\sqrt{186}-5\sqrt{13} =\sqrt{186} - \sqrt{5^2 \cdot 13}=\)
\(=\sqrt{186} - \sqrt{25\cdot13}=\)
\(=\sqrt{186} - \sqrt{325}<0\).
| × | 2 | 5 | |
| 1 | 3 | ||
| + | 7 | 5 | |
| 2 | 5 | ||
| 3 | 2 | 5 |
и) \(\sqrt{ -\sqrt{186}+5\sqrt{7}}\) - не имеет смысла.
\(-\sqrt{186}+5\sqrt{7}= 5\sqrt{7} - \sqrt{186}=\)
\(=\sqrt{5^2\cdot7} - \sqrt{186} =\)
\(=\sqrt{25\cdot7} - \sqrt{186}=\)
\(=\sqrt{175} - \sqrt{186}<0\).
к) \(\sqrt{ \sqrt{56}-4\sqrt{2}}\) - имеет смысл.
\(\sqrt{56}-4\sqrt{2} = \sqrt{56} - \sqrt{4^2\cdot2}=\)
\(=\sqrt{56} - \sqrt{16\cdot2} = \sqrt{56} - \sqrt{32} > 0\)
л) \(\sqrt{ \sqrt{ 42}-6\sqrt{5}}\) - не имеет смысла.
\(\sqrt{42}-6\sqrt{5} = \sqrt{42}-\sqrt{6^2\cdot5}=\)
\(=\sqrt{ 42}-\sqrt{36\cdot5}= \)
\(=\sqrt{ 42}-\sqrt{180}<0\).
м) \(\sqrt{ \sqrt{72}-6\sqrt{2}}\) - имеет смысл.
\(\sqrt{72}-6\sqrt{2} = \sqrt{72}-\sqrt{6^2\cdot2}=\)
\(\sqrt{72}-\sqrt{36\cdot2}= \sqrt{72}-\sqrt{72}=0\).
Пояснения:
Использованные приемы:
- Выражение \(\sqrt x\) имеет смысл только тогда, когда \(x\geqslant0\).
- Сравнение корней:
\(\sqrt x \geqslant \sqrt y\), только в том случае, когда \(x \geqslant y\).
- Чтобы внести числовой множитель \(k\) под знак корня, каждый внешний числовой множитель \(k\) возводят в квадрат и умножают на подкоренное выражение:
\( k\sqrt{A} = \sqrt{k^2\cdot A}. \)
№404 учебника 2013-2022 (стр. 96):
а) \( \sqrt{2304} = \sqrt{2^8 \cdot 3^2} =\)
\(=\sqrt{(2^4)^2}\cdot \sqrt{3^2} = |2^4|\cdot|3| =\)
\(=16\cdot3 = 48. \)

б) \( \sqrt{18225} = \sqrt{3^6\cdot5^2} =\)
\(= \sqrt{(3^3)^2}\cdot \sqrt{5^2} = |3^3|\cdot|5| = \)
\(=27\cdot5 = 135. \)
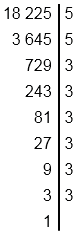
в) \( \sqrt{254016} = \sqrt{2^6\cdot3^4\cdot7^2} =\)
\(=\sqrt{(2^3)^2}\cdot\sqrt{(3^2)^2}\cdot\sqrt{7^2} =\)
\(=|2^3|\cdot|3^2|\cdot|7| = 8\cdot9\cdot7 = 504. \)
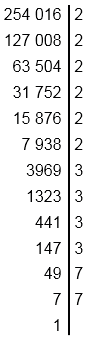
Пояснения:
– Свойство корня из степени:
\( \sqrt{(x^n)^2} = |x^n|.\)
– Свойство корня из произведения:
\(\sqrt{ab} = \sqrt{a}\cdot\sqrt{b}\).
– Свойство степени:
\((a^m)^n = a^{mn}\).
– Определение модуля:
\(|a| = a\), при \(a \ge 0\);
\(|a| = -a\), при \(a \le 0\).
– В каждом случае разложили число на простые множители, сгруппировали их в чётные степени и вынесли из-под корня.
– Конечный результат получен перемножением вынесенных из-под корня простых степеней.
Вернуться к содержанию учебника